3. Modeling A

3.1. Characteristics of modeling

We use C_ PLAN modeling.

3.2. Characteristics of the mesh

The mesh contains 121 elements of type QUAD4.

3.3. Tested sizes and results

The maximum and minimum stresses on the plate are tested for field SIEF_ELNO:

Identification	Reference type
\(\mathit{MAX}\) - \(\mathit{SIXX}\)	“NON_REGRESSION”
\(\mathit{MIN}\) - \(\mathit{SIXX}\)	“NON_REGRESSION”
\(\mathit{MAX}\) - \(\mathit{SIXY}\)	“NON_REGRESSION”
\(\mathit{MIN}\) - \(\mathit{SIXY}\)	“NON_REGRESSION”

The maximum and minimum stresses on the plate are tested for field SIGM_ELNO calculated underground by the operator CALC_ERREUR:

Identification	Reference type
\(\mathit{MAX}\) - \(\mathit{SIXX}\)	“NON_REGRESSION”
\(\mathit{MIN}\) - \(\mathit{SIXX}\)	“NON_REGRESSION”
\(\mathit{MAX}\) - \(\mathit{SIXY}\)	“NON_REGRESSION”
\(\mathit{MIN}\) - \(\mathit{SIXY}\)	“NON_REGRESSION”

We test the minimum and maximum constraints on the field plate SISE_ELNO (node of the sub-elements X- FEM) calculated underground by the operator CALC_ERREUR:

Identification	Reference type	Reference value	Precision
\(\mathit{MAX}\) - \(X4\)	“NON_REGRESSION”	0.812078942873 MPa	1E -04%
\(\mathit{MIN}\) - \(X4\)	“NON_REGRESSION”	-0.510118026455 MPa	1E -04%

Finally we test the field for error estimator ERME_ELEM:

Identification	Reference type	Reference value	Precision
\(\mathit{MAX}\) - \(\mathit{ERREST}\)	“NON_REGRESSION”	0.000698457464821	1E -04%
\(\mathit{MIN}\) - \(\mathit{ERREST}\)	“NON_REGRESSION”	3.49704197058E-06	1E -04%

3.4. notes

The constraints obtained calculated at the nodes of the mesh by CALC_ERREUR and by CALC_CHAMP are indeed the same.

The stress field is resolved at Gauss points:

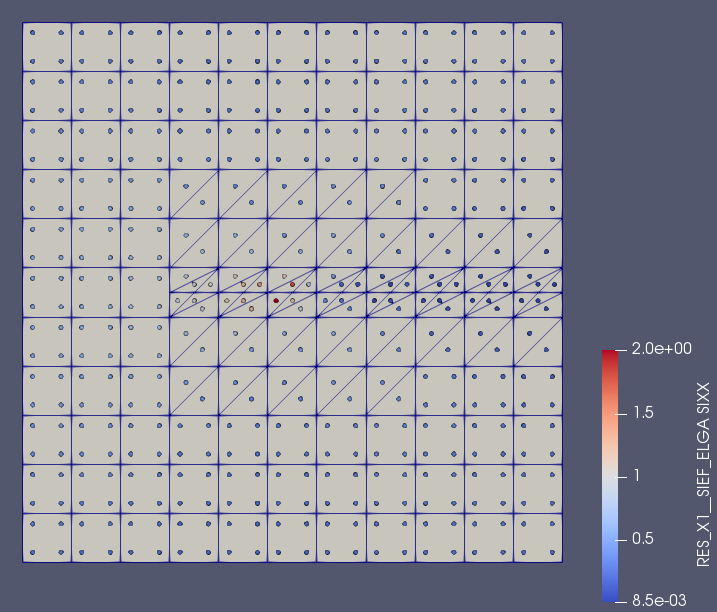
The smoothing done by calculating the stresses at the nodes introduces errors that cause the CALC_ERREURàsous -operator to estimate the error of the asymptotic field at the bottom of the crack.