1. Reference problem#

1.1. Geometry#

We consider a disk of radius \(\mathrm{100mm}\), embedded at its edges, and containing a horizontal crack of \(\mathrm{23mm}\), one of whose points is in the center of the disk. The presents this geometry.

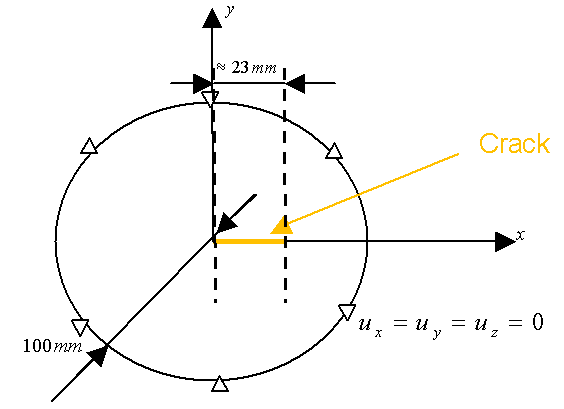
_images/10000000000002340000019968BA48067ED88EB3.png

Figure 1.1: Disc geometry.

.

1.2. Material properties#

Young’s module: \(E=210000\mathrm{MPa}\)

Poisson’s ratio: \(\nu =\mathrm{0,3}\)

Coefficient of thermal expansion: \(\alpha ={10}^{-5}{K}^{-1}\)

1.3. Boundary conditions and loads#

The disc is completely embedded on its edge.

It is subject to a field of initial stresses obtained by applying a thermal load with a strong gradient in the horizontal direction (see and).

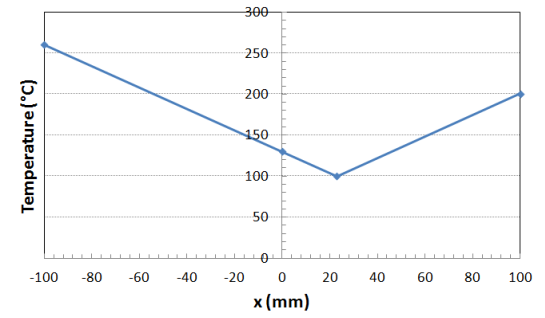
_images/10000000000002210000013E228E42EC6C041CD3.png

Figure 1.2: Temperature gradient applied to the embedded disc.

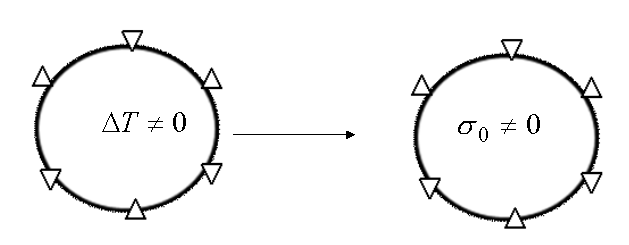
_images/1000000000000275000000F57537E6AC30CDA8CB.png

Figure 1.3: Creation of the initial constraints field.

1.4. Benchmark solution#

The reference solution is that obtained by applying the thermal load directly to the cracked disk with no initial state. In fact, since the behavior is elastic, the principle of superposition applies and the results in the presence of thermal loading without initial constraints and in the absence of thermal with initial constraints are equivalent, as summarized in.

_images/10000000000002150000022E7555234486A4683F.png

Figure 1.4: Equivalence of loads.