2. Reference solution#
2.1. Torsional moment#
An analytical solution for the torsional moment is easily found by calculating the Strength of Materials.
Let the \(\mathit{AB}\) beam of length \(L\), embedded in \(A\), if we apply a torsional moment \(\mathit{mt}\) at a point \(C\) of \(\mathrm{[}\mathit{AB}\mathrm{]}\) then the moment resulting in \(A\) is \(\mathit{mt}\). So the reaction at the moment is \(\mathrm{-}\mathit{mt}\).
By applying a linear torsional moment, distributed over the beam, equal to \({\mathit{mt}}_{A}\) in \(A\) and to \({\mathit{mt}}_{B}\) in \(B\), we obtain the moment reaction \({M}_{A}\) in \(A\):
\({M}_{A}\mathrm{=}\mathrm{-}{\mathrm{\int }}_{0}^{L}{\mathit{mt}}_{A}+\frac{({\mathit{mt}}_{B}\mathrm{-}{\mathit{mt}}_{A})}{L}x\mathit{dx}\)
\({M}_{A}\mathrm{=}\mathrm{-}L\frac{({\mathit{mt}}_{A}+{\mathit{mt}}_{B})}{2}\)
2.2. Bending moment#
The Material Strength Forms provide reference results for a moment according to \(Z\) applied to point \(C\) of a \(\mathit{AB}\) beam of length \(L\) embedded in \(A\) and supported according to \(Y\) in \(B\).
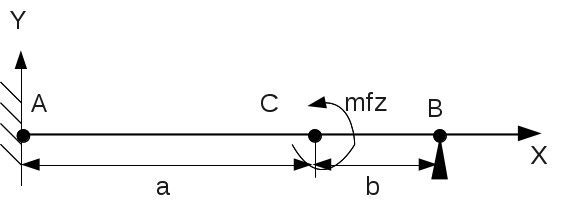
\({R}_{A}\mathrm{=}\mathrm{-}{R}_{B}\mathrm{=}\frac{3\mathit{mfz}({L}^{2}\mathrm{-}{b}^{2})}{{\mathrm{2L}}^{3}}\)
\({M}_{A}\mathrm{=}\frac{\mathit{mfz}({L}^{2}\mathrm{-}{\mathrm{3b}}^{2})}{{\mathrm{2L}}^{2}}\)
where \({R}_{A}\) is the supporting reaction and \({M}_{A}\) is the moment, in \(A\).
By applying a linear bending moment, distributed over the beam, equal to \({\mathit{mf}}_{A}\) in \(A\) and to \({\mathit{mf}}_{B}\) in \(B\), we obtain:
\({R}_{A}=-{R}_{B}=\frac{3}{{\mathrm{2L}}^{3}}\underset{0}{\overset{L}{\int }}({\mathit{mf}}_{A}+\frac{({\mathit{mf}}_{B}-{\mathit{mf}}_{A})}{L}x)({L}^{2}-{(L-x)}^{2})\mathit{dx}\)
\({M}_{A}=\frac{1}{{\mathrm{2L}}^{2}}\underset{0}{\overset{L}{\int }}({\mathit{mf}}_{A}+\frac{({\mathit{mf}}_{B}-{\mathit{mf}}_{A})}{L}x)({L}^{2}-3{(L-x)}^{2})\mathit{dx}\)
What results after integration:
\({R}_{A}\mathrm{=}\mathrm{-}{R}_{B}\mathrm{=}\frac{3{\mathit{mf}}_{A}+5{\mathit{mf}}_{B}}{8}\)
\({M}_{A}\mathrm{=}L\frac{{\mathit{mf}}_{B}\mathrm{-}{\mathit{mf}}_{A}}{8}\)
Note: If you go into plan \(\mathit{XOZ}\) with the application of a moment according to \(Y\), you have to multiply the reactions by \(\mathrm{-}1\).
2.3. Uncertainty about the solution#
None.