1. Reference problem#
1.1. Geometry#
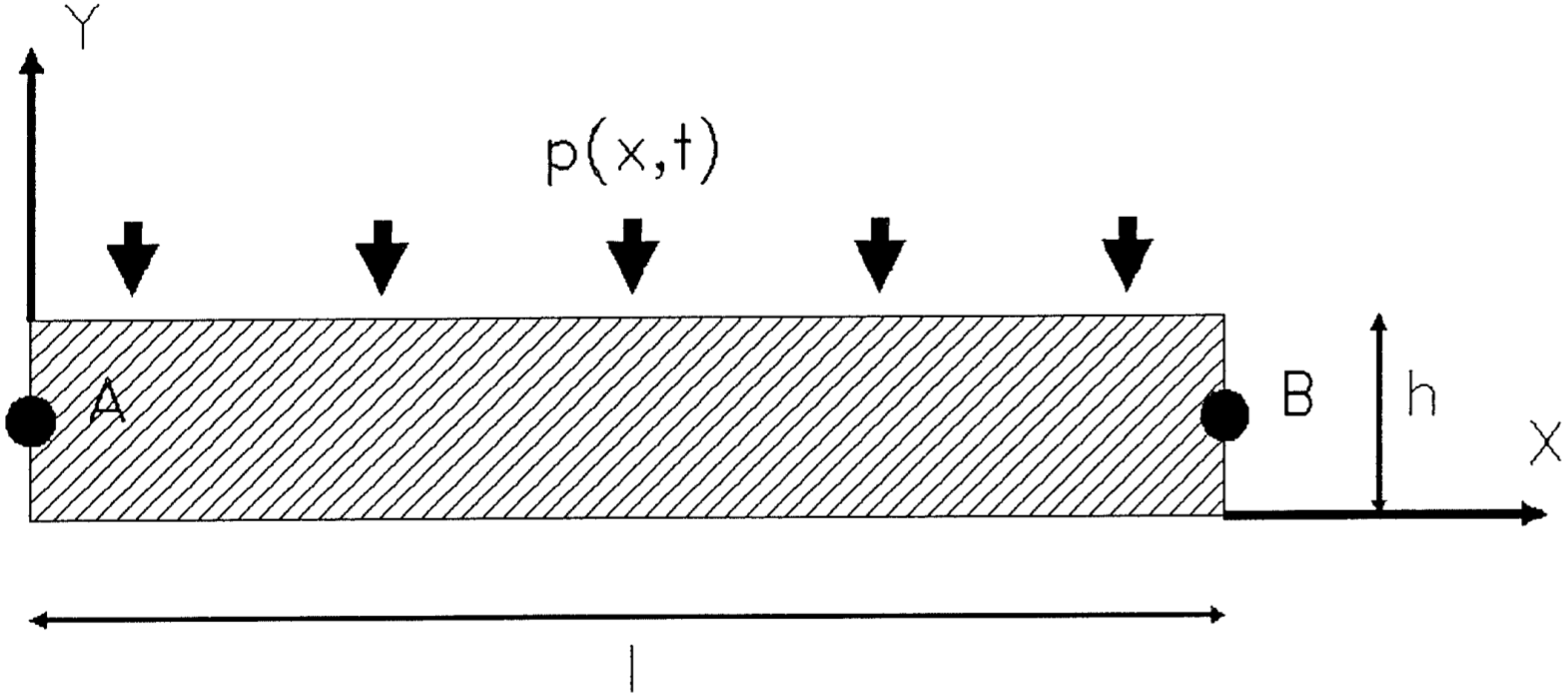
Figure 1.1-1: Problem geometry
Height: \(h=0.2\text{m}\)
Width: \(b=0.1\text{m}\)
Length: \(L=2\text{m}\)
Section: \(A=b\times h=0.02\text{m}\)
Inertia: \(I=\frac{b\times {h}^{3}}{12}=1.66\times {10}^{-5}\text{m}\)
Section reduction coefficient \(k\text{'}=\frac{5}{6}\)
1.2. Material properties#
Young’s module |
\(E=2.1\times {10}^{11}\mathit{Pa}\) |
Poisson’s Ratio |
\(\nu =0.3\) |
Density |
\(\rho =7800.0{\mathit{kg.m}}^{-3}\) |
Shear modulus |
\(G=\frac{E}{2(1+\nu )}=8.076\times {10}^{10}\text{Pa}\) |
Rayleigh damping coefficients |
\(\alpha =1.6\times {10}^{-5}\text{s}\) and \(\beta =16{\text{s}}^{-1}\) |
1.3. Boundary conditions and loads#
Only the flexure in the \(\mathit{XY}\) plane and the extension along the \(X\) axis are allowed. Since the model is solid, the boundary conditions differ somewhat from those that would be imposed on a beam model.
Imposed displacement:
In \(X=0\), \(Y=h/2\) |
|
In \(X=L\), \(Y=h/2\) |
|
In \(Z=b/2\) |
|
To the previous conditions, we add the flatness constraint of the sections in \(X=0\) and \(X=L\). This constraint can be expressed as follows. Let’s designate \({x}^{T}=(X,Y,Z)\) the coordinate vector and \({u}^{T}=(\mathit{DX},\mathit{DY},\mathit{DZ})\) the displacement vector; the position of a point is identified by the vector \(x{\text{'}}^{T}={x}^{T}+{u}^{T}=(X\text{'},Y\text{'},Z\text{'})\). Let \(A\), \(B\), and \(C\) be three non-aligned points in the section. Any point \(P\) is subject to the condition:
\(∣\begin{array}{cccc}X{\text{'}}_{P}& Y{\text{'}}_{P}& Z{\text{'}}_{P}& 1\\ X{\text{'}}_{A}& Y{\text{'}}_{A}& Z{\text{'}}_{A}& 1\\ X{\text{'}}_{B}& Y{\text{'}}_{B}& Z{\text{'}}_{B}& 1\\ X{\text{'}}_{C}& Y{\text{'}}_{C}& Z{\text{'}}_{C}& 1\end{array}∣=0\)
Imposed force:
In \(Y=h\), for all \(X\), the load is defined by:
\(p(x,t)=p(x)\mathrm{sin}(\omega t)\)
with \(p(x)={p}_{0}=5.0\times {10}^{4}{\text{N.m}}^{-1}\) and \(\omega =2000\pi {\text{rd.s}}^{-1}\).