1. Reference problem#
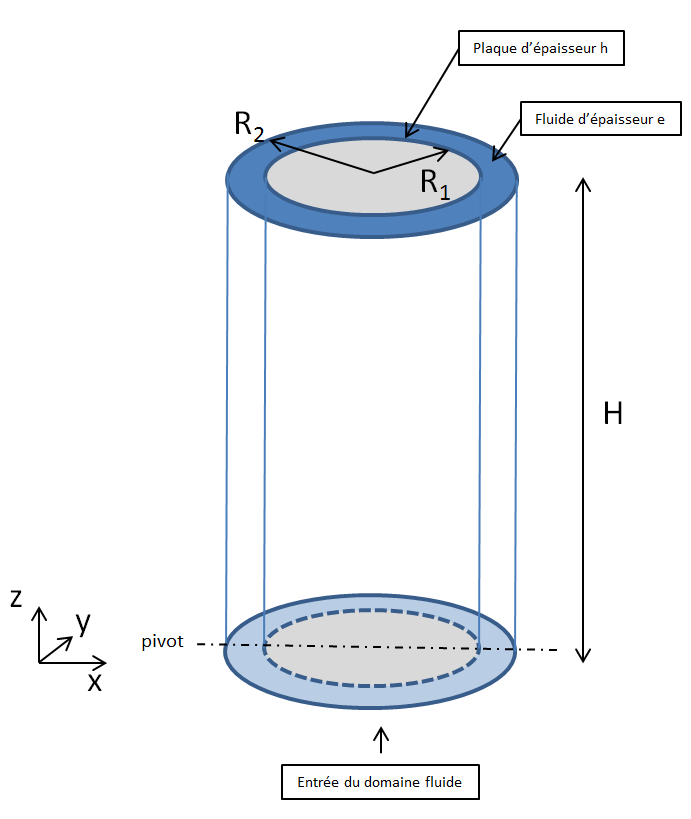
1.1. Geometry#
Cylinder height \(H\mathrm{=}10m\)
Inner cylinder radius \({R}_{1}\mathrm{=}0.5m\)
fluid thickness \(e\mathrm{=}1m\) (External cylinder radius \({R}_{2}\mathrm{=}2m\))
plate thickness \(h=0.5m\)
1.2. Material properties#
Structure: \({\rho }_{s}\mathrm{=}7800\mathit{kg}\mathrm{/}{m}^{3}\), \(E\mathrm{=}2.1{10}^{11}\mathit{Pa}\), \(\nu \mathrm{=}0.3\) (steel).
1.3. Boundary conditions and loads#
Structure:
the cylinder is subject to balancing around a pivot located upstream of the axial annular flow along this cylinder:
\({X}_{1}\mathrm{=}z\)
Parameter for spectrum calculation:
Cutoff frequency: \(F\mathrm{=}\mathrm{15Hz}\)
Constant for the magnitude of the pressure spectrum \(K\mathrm{=}\mathrm{3,4}{e}^{\mathrm{-}5}{s}^{1\mathrm{/}2}\mathrm{/}{m}^{3\mathrm{/}2}\)
Hydraulic diameter for the amplitude of the pressure spectrum \(d\mathrm{=}\mathrm{1,5}\)
Coefficient of the convective speed of vortices in the axial direction (direction of flow) \(\alpha \mathrm{=}\mathrm{0,65}\)
The correlation lengths for turbulence in the axial and orthoradial directions are equal to \(\lambda \mathrm{=} \lambda\text{'} \mathrm{=} \mathrm{5}\)