3. Modeling A#
3.1. Characteristics of modeling#
The beam is cut into two parts of equal dimensions. Each substructure under consideration is meshed into segments to which elements of type POU_D_T are assigned.
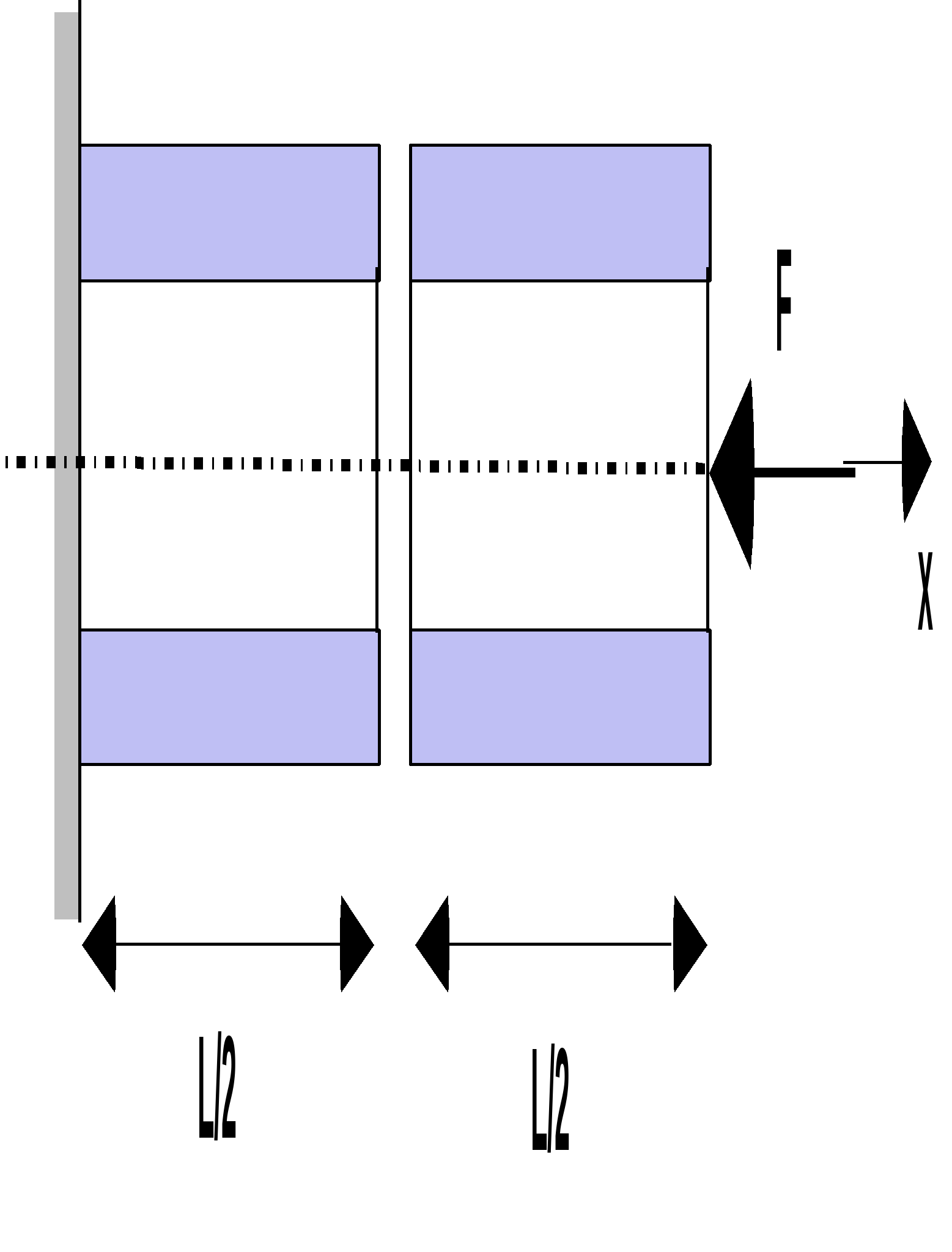
The structure is studied using the transient substructuration method with « Craig-Bampton » interfaces (blocked interfaces).
The modal base used is composed of 4 eigenmodes for the left substructure, 5 eigenmodes for the right substructure to which are added the constrained modes associated with the interface degrees of freedom (2 in number).
Projection base of the left substructure:

Basis of projection of the substructure on the right:
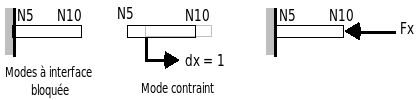
3.2. Characteristics of meshes#
The mesh of the complete beam to perform the reference calculation has the following characteristics:
Aster mesh file (.mail)
Number of knots = 11
Number of stitches = 10 SEG2
The mesh of the half-beam to perform the calculation by substructuring, has the following characteristics:
Ideas file (.msup)
Number of knots = 6
Number of stitches = 5 SEG2
3.3. Tested features#
We test the dynamic calculation functionalities by substructuring as well as the reproduction in physical space.
3.4. Tested sizes and results#
The values are restored on a skeleton mesh made up of the two substructures. The initial mesh, which contains 6 nodes, is duplicated to create the substructure on the right. The end node therefore corresponds to node 12.
Identification |
Reference (full beam) |
Sub-structure |
Difference (%) |
|
Node 12: move \((m)\) |
—6.2818E—7 |
—6.2818E—7 |
< 0.1 |
|
Node 12: speed \(({\mathrm{m.s}}^{-1})\) |
2.0957E—3 |
2.0957E—3 |
2.0957E—3 |
< 0.1 |
Node 12: acceleration \(({\mathrm{m.s}}^{-2})\) |
1.1139E+1 |
1.1139E+1 |
< 0.1 |
3.5. notes#
It is surprising that the reference adopted corresponds to the complete beam modelled by 10 elements and not to the analytical solution. It turns out that the development of the serial solution of natural modes converges very slowly: the modal solution is here very far from the theoretical solution. The relevant comparison is therefore the one selected.
The calculation by modal recombination is carried out on the complete modal basis of the structure (11 modes) taking into account the discretization adopted. Likewise, the dimension of the projection base used for the calculation by dynamic substructuring is 11 (left substructure: 4 natural modes + 1 constrained mode; right substructure: 5 natural modes + 1 constrained mode). It is therefore normal to obtain an excellent agreement between the modeling of the complete beam and that of the beam divided into two substructures.