2. Benchmark solution#
2.1. Calculation method used for the reference solution#
The reference results were obtained both experimentally [1] and with the code HERCULE [2]. The finite element model used is identical to that used for modeling A performed with*Code_Aster*.
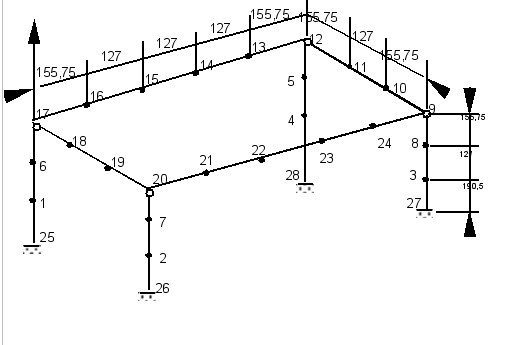
|
|
The geometric dimensions used in calculations with HERCULE are very slightly different from those shown in §1.1:
\(L=\mathrm{692.50}\mathrm{mm}\); \(l=\mathrm{438.50}\mathrm{mm}\); \(H=\mathrm{473.25}\mathrm{mm}\)
2.2. Benchmark results#
Natural frequencies
Move to the points forming the corners of the table,
Support reactions to anchorages,
Internal forces at the « corners ».
Identification |
Reference [] experimental |
Reference [] Hercule |
Effective mass (% of total mass) |
||
Fashion |
Frequency (\(\mathrm{Hz}\)) |
Frequency (\(\mathrm{Hz}\)) |
\(X\) |
\(Y\) |
\(Z\) |
1 |
110.0 |
110.857 |
94.2 |
0.0 |
0.0 |
2 |
117.0 |
115.471 |
0.0 |
0.0 |
94.4 |
3 |
134.0 |
135.936 |
0.0 |
0.0 |
0.0 |
4 |
214.0 |
213.541 |
0.0 |
0.0 |
0.0 |
5 |
416.0 |
417.332 |
0.0 |
0.0 |
0.0 |
6 |
434.813 |
0.0 |
24.1 |
0.0 |
|
7 |
464.097 |
0.0 |
0.0 |
0.0 |
|
8 |
553.0 |
557.262 |
0.0 |
0.0 |
0.3 |
9 |
821.0 |
821.746 |
0.0 |
18.0 |
0.0 |
10 |
847.071 |
0.0 |
0.0 |
0.0 |
|
11 |
927.0 |
978.174 |
1.6 |
0.0 |
0.0 |
12 |
991.842 |
0.0 |
2.2 |
0.0 |
|
13 |
1021.669 |
1.8 |
0.0 |
0.0 |
|
14 |
1040.240 |
0.0 |
0.0 |
0.0 |
|
15 |
1056.948 |
0.0 |
0.0 |
0.2 |
|
16 |
1088.861 |
0.0 |
18.8 |
0.0 |
|
17 |
1093.157 |
1.2 |
0.0 |
0.0 |
|
18 |
1107.870 |
0.0 |
0.0 |
0.0 |
|
Identification |
Values obtained with combination |
|
quadratic directions of excitations |
Of NEWMARK of the directions of the excitations |
|
Displacement: |
||
\(\mathrm{N17}\) \(\mathrm{DX}(m)\) |
3.4246E-04 |
3.4265E-04 |
\(\mathrm{DY}(m)\) |
4.3562E-06 |
4.8392E-06 |
\(\mathrm{DZ}(m)\) |
3.0321E-04 |
3.0324E-04 |
\(\mathrm{DRX}(\mathrm{rad})\) |
3.7031E-04 |
3.7612E-04 |
\(\mathrm{DRY}(\mathrm{rad})\) |
4.7665E-05 |
5.2602E-05 |
\(\mathrm{DRZ}(\mathrm{rad})\) |
5.1104E-04 |
5.2310E-04 |
Reactions: |
||
\(\mathrm{N25}\) \(\mathrm{FX}(N)\) |
1.2536E+03 |
1.2790E+03 |
\(\mathrm{FY}(N)\) |
1.2473E+03 |
1.3868E+03 |
\(\mathrm{FZ}(N)\) |
1.2196E+03 |
1.2441E+03 |
\(\mathrm{MX}(\mathrm{N.m})\) |
3.2474E+02 |
3.2789E+02 |
\(\mathrm{MY}(\mathrm{N.m})\) |
4.1310E+00 |
4.5579E+00 |
\(\mathrm{MZ}(\mathrm{N.m})\) |
3.4846E+02 |
3.5199E+02 |
Efforts: |
||
\(1019\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
1.1312E+03 |
1.1486E+03 |
\(\mathrm{FY}(N)\) |
1.2431E+03 |
1.3793E+03 |
\(\mathrm{FZ}(N)\) |
1.0982E+03 |
1.1141E+03 |
\(\mathrm{MX}(\mathrm{N.m})\) |
2.2833E+02 |
2.2982E+02 |
\(\mathrm{MY}(\mathrm{N.m})\) |
4.1301E+00 |
4.5580E+00 |
\(\mathrm{MZ}(\mathrm{N.m})\) |
2.2068E+02 |
2.2537E+02 |
\(1009\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
1.8813E+02 |
2.0079E+02 |
\(\mathrm{FY}(N)\) |
1.0419E+03 |
1.0650E+03 |
\(\mathrm{FZ}(N)\) |
1.3175E+02 |
1.4833E+02 |
\(\mathrm{MX}(\mathrm{N.m})\) |
2.2833E+02 |
2.2975E+02 |
\(\mathrm{MY}(\mathrm{N.m})\) |
2.9165E+01 |
3.2490E+01 |
\(\mathrm{MZ}(\mathrm{N.m})\) |
1.6408E-01 |
1.6400E-01 |
\(1008\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
2.9587E+02 |
3.3579E+02 |
\(\mathrm{FY}(N)\) |
6.3879E+02 |
6.7526E+02 |
\(\mathrm{FZ}(N)\) |
2.6539E+02 |
2.7947E+02 |
\(\mathrm{MX}(\mathrm{N.m})\) |
1.8400E-01 |
1.8500E-01 |
\(\mathrm{MY}(\mathrm{N.m})\) |
3.2361E+01 |
3.5570E+01 |
\(\mathrm{MZ}(\mathrm{N.m})\) |
2.2068E+02 |
2.2535E+02 |
notes
The movements of corners \((\mathrm{N9},\mathrm{N12},\mathrm{N17},\mathrm{N20})\) are the same,
The reactions to the \((\mathrm{N25},\mathrm{N26},\mathrm{N27},\mathrm{N28})\) supporters are the same,
Generalized efforts are expressed in the global benchmark.
2.3. Bibliographical references#
NEUBERT V.H. and EZELL W. H.: Dynamic behavior of a foundation like structure. ASME Colloquium on Mechanical Impedance Methods for Mechanical Vibrations, pp. 77-86, 1958.
HERCULE: finite element calculation code for building structures developed by SOCOTEC.