4. B modeling#
4.1. Characteristics of modeling#
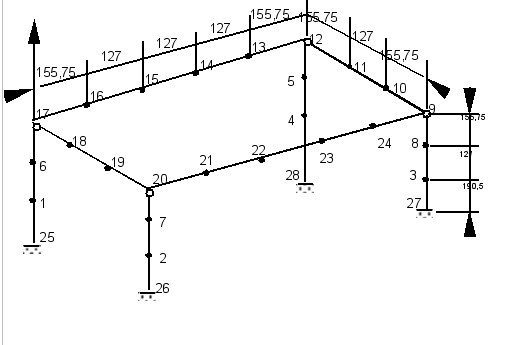
Mesh |
\(\mathrm{E3}\) |
: |
\(\mathrm{N6}-\mathrm{N17}\) |
\(\mathrm{E4}\) |
: |
\(\mathrm{N17}-\mathrm{N18}\) |
|
\(\mathrm{E19}\) |
: |
\(\mathrm{N17}-\mathrm{N16}\) |
Masses of corners |
: |
\(4.444\mathrm{kg}\) |
Intermediate masses |
: |
\(0.783\mathrm{kg}\) |
4.2. Characteristics of the mesh#
Number of knots: 28
Number of meshes and types: 52 (28 MECA_POU_D_T and 24 MECA_DIS_T_N)
4.3. notes#
The modes are normalized to the mass generalized to 1.
The overall response is obtained by quadratic combination of the modes, then successively a quadratic combination and a Newmark combination of the directions of the excitations.
4.4. Tested values: frequencies#
4.5. Values tested with quadratic combination of the directions of the excitations#
Identification |
Reference |
% tolerance |
Displacement: |
||
\(\mathrm{N17}\) \(\mathrm{DX}(m)\) |
3.4246E-04 |
|
\(\mathrm{DY}(m)\) |
4.3562E-06 |
|
\(\mathrm{DZ}(m)\) |
3.0321E-04 |
|
\(\mathrm{DRX}(\mathrm{rad})\) |
3.7031E-04 |
|
\(\mathrm{DRY}(\mathrm{rad})\) |
4.7665E-05 |
|
\(\mathrm{DRZ}(\mathrm{rad})\) |
5.1104E-04 |
|
Reactions REAC_NODA: |
||
\(\mathrm{N25}\) \(\mathrm{FX}(N)\) |
1.2536E+03 |
|
\(\mathrm{FY}(N)\) |
1.2473E+03 |
|
\(\mathrm{FZ}(N)\) |
1.2196E+03 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
3.2474E+02 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
4.1310E+00 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
3.4846E+02 |
|
Efforts EFGE_ELNO: |
||
\(\mathrm{E3}\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
1.1312E+03 |
|
\(\mathrm{FY}(N)\) |
1.2431E+03 |
|
\(\mathrm{FZ}(N)\) |
1.0982E+03 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
2.2833E+02 |
-2. |
\(\mathrm{MY}(\mathrm{N.m})\) |
4.1301E+00 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
2.2068E+02 |
|
\(\mathrm{E4}\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
1.8813E+02 |
|
\(\mathrm{FY}(N)\) |
1.0419E+03 |
|
\(\mathrm{FZ}(N)\) |
1.3175E+02 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
2.2833E+02 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
2.9165E+01 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
1.6408E-01 |
|
\(\mathrm{E19}\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
2.9587E+02 |
|
\(\mathrm{FY}(N)\) |
6.3879E+02 |
|
\(\mathrm{FZ}(N)\) |
2.6539E+02 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
1.8400E-01 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
3.2361E+01 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
2.2068E+02 |
4.6. Values tested with combination of NEWMARK of the directions of the excitations#
Identification |
Reference |
% tolerance |
Displacement: |
||
\(\mathrm{N17}\) \(\mathrm{DX}(m)\) |
3.4265E-04 |
|
\(\mathrm{DY}(m)\) |
4.8392E-06 |
|
\(\mathrm{DZ}(m)\) |
3.0324E-04 |
|
\(\mathrm{DRX}(\mathrm{rad})\) |
3.7612E-04 |
2. |
\(\mathrm{DRY}(\mathrm{rad})\) |
5.2602E-05 |
|
\(\mathrm{DRZ}(\mathrm{rad})\) |
5.2310E-04 |
|
Reactions REAC_NODA: |
||
\(\mathrm{N25}\) \(\mathrm{FX}(N)\) |
1.2790E+03 |
|
\(\mathrm{FY}(N)\) |
1.3868E+03 |
|
\(\mathrm{FZ}(N)\) |
1.2441E+03 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
3.2789E+02 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
4.5579E+00 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
3.5199E+02 |
|
Efforts EFGE_ELNO: |
||
\(\mathrm{E3}\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
1.1486E+03 |
|
\(\mathrm{FY}(N)\) |
1.3793E+03 |
|
\(\mathrm{FZ}(N)\) |
1.1141E+03 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
2.2982E+02 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
4.5580E+00 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
2.2537E+02 |
|
\(\mathit{E4}\) \(\mathit{N17}\) \(\mathit{FX}(N)\) |
2.0079E+02 |
|
\(\mathrm{FY}(N)\) |
1.0650E+03 |
|
\(\mathrm{FZ}(N)\) |
1.4833E+02 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
2.2975E+02 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
3.2490E+01 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
1.6400E-01 |
|
\(\mathrm{E19}\) \(\mathrm{N17}\) \(\mathrm{FX}(N)\) |
3.3579E+02 |
|
\(\mathrm{FY}(N)\) |
6.7526E+02 |
|
\(\mathrm{FZ}(N)\) |
2.7947E+02 |
|
\(\mathrm{MX}(\mathrm{N.m})\) |
1.8500E-01 |
|
\(\mathrm{MY}(\mathrm{N.m})\) |
3.5570E+01 |
|
\(\mathrm{MZ}(\mathrm{N.m})\) |
2.2535E+02 |
The movements of corners \((\mathrm{N9},\mathrm{N12},\mathrm{N17},\mathrm{N20})\) are the same,
The reactions to the \((\mathrm{N25},\mathrm{N26},\mathrm{N27},\mathrm{N28})\) supporters are the same,
Generalized efforts are expressed in the global benchmark.