1. Introduction#
Among the classical approaches to fracture mechanics, there are damage laws, for which the loss of mechanical strength is described by the degradation of the volume properties of the material, and two approaches that concentrate this degradation on a surface: the Griffith approach [bib1], and cohesive zone models (CZM). The Griffith model consists in performing a mechanical calculation on a cracked domain, the crack being free of stresses, and in calculating energy quantities (energy release rate \(G\) and stress intensity factors \({K}_{I},{K}_{\mathit{II}}\), see documentation [R7.02.01] and [R7.02.05]) that trigger propagation if a threshold quantity \({G}_{c}\) (which is a material property) is reached.
Despite this simplicity, this method has drawbacks for some applications:
If the size of the crack development zone becomes comparable to the characteristic lengths of the model (size of the structure, initial crack length, etc.), the response of the structure has a scale effect that the Griffith model fails to reproduce. This is generally the case for*concrete and geomaterials, *as well as*short cracks.
Since the Griffith propagation criterion is implicit, it is very difficult to determine the advance of the front as a \(G={G}_{c}\) curve. As explained by Fries [bib11], explicit, highly empirical criteria should be used instead.
In CZM, \({t}_{c}\) cohesive forces are exerted between the lips of the crack. They obey a softening relationship of the displacement jump \(⟦u⟧\), so they are worth \(0\) when the crack is fully open (see fig.).
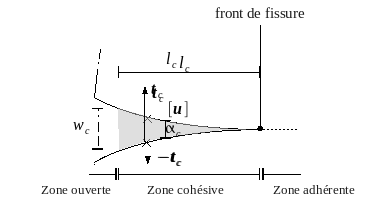
Figure 1-1: Cohesive zone model.
In this context, the extended finite element method (XFEM) is a numerical technique that makes it possible to insert surfaces of discontinuity through the elements [bib2], and therefore to avoid the constraint of meshing them. This is particularly useful for crack propagation studies over an unknown path: remeshing problems are avoided.
Three types of cohesive laws are available for the X- FEM elements:
regularized cohesive laws (i.e. with finite initial stiffness) for linear finite elements CZM_LIN_REG and CZM_EXP_REG. These are the first laws introduced and the simplest, but they present convergence difficulties as soon as the adherent zone becomes large.
mixed cohesive laws (i.e. with infinite initial stiffness) for quadratic finite elements CZM_OUV_MIX and CZM_TAC_MIX. They are more robust and accurate, but reserved for quadratic elements.
the mixed cohesive law CZM_LIN_MIX, for linear finite elements.*Propagation studies over an unknown path are only feasible with the law CZM_LIN_MIX.
In this document, we start by writing the strong formulation of the problem and by presenting the cohesive force/displacement jump relationships for the three cohesive laws (cf. [§2]). We then write the variational formulation of the problem (cf. [§3]). We explain the resolution of the problem by a Newton-Raphson method (cf. [§4]), and present the linearization of the variational formulation. We write the finite element discretization of the problem, by giving the matrix expressions of the tangent matrix and the second-member vectors (cf. [§5]). Finally, we detail the procedure for studying the propagation of cohesive cracks over an unknown path (cf. [§6]).