2. Problem overview#

2.1. Definition of the field of study#

Let \(\mathrm{\Omega }\subset {\mathrm{ℝ}}^{d}\) with \(d\in \{\mathrm{2,}3\}\) be a domain that is entirely crossed by a crack or a permeable interface. Let \(n\) be the external normal at the \(\partial \Omega\) border of the domain, and \({n}_{c}\) that of the interface \({\Gamma }_{c}\).

It is possible to break down:

  • the border of domain \(\Omega\) in \(\partial \Omega ={\Gamma }_{u}\cup {\Gamma }_{t}\cup {\Gamma }_{p}\cup {\Gamma }_{F}\) where limit conditions (of the Dirichlet and Neumann type) for hydrodynamics (on \({\Gamma }_{p}\) and \({\Gamma }_{F}\)) and for mechanics (on \({\Gamma }_{u}\) and \({\Gamma }_{t}\)) are imposed,

  • the interface in \({\Gamma }_{c}={\Gamma }_{f}\cup {\Gamma }_{1}\cup {\Gamma }_{2}\) where \({\Gamma }_{1}\) and \({\Gamma }_{2}\) represent the lips of discontinuity. Flow conditions are imposed on \({\Gamma }_{1}\), \({\Gamma }_{2}\) and \({\Gamma }_{f}\) and cohesive surface forces are imposed on \({\Gamma }_{1}\) and \({\Gamma }_{2}\).

The data is a symbolic representation of the conditions imposed on the border of the domain.

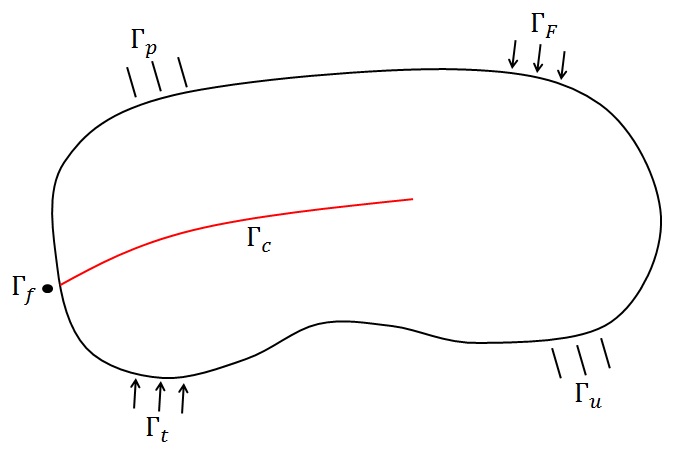
_images/10000000000002AB000001C74E024DFF31F024C3.jpg

Figure 2.1-1: Imposition of boundary conditions

2.2. Assumptions and notations#

A porous medium saturated with liquid (generally water) is considered. The coupling law associated in Code_Aster is therefore LIQU_SATU (for more details refer to the model instructions THM [U2.04.05]). On the other hand, there is a longitudinal flow of fluid at the interface. Assuming that it is permeable, fluid exchanges take place between the massif (part of \(\Omega\) that is not the interface) and the interface. They are represented on the.

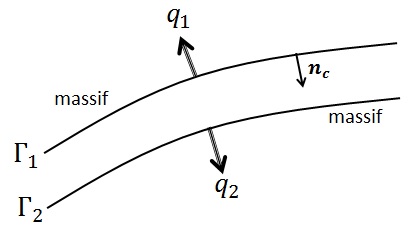
_images/100000000000019A000000E823063B816F477D5E.jpg

Figure 2.2-1: Orientation of exchanges between the massif and the discontinuity

\({q}_{1}\) and \({q}_{2}\) are the flows due to exchanges between the massif and the interface, and are expressed in \({\mathit{kg.m}}^{\text{-2}}\mathrm{.}{s}^{\text{-1}}\). These flows come from the interface and are directed respectively to the upper and lower parts of the massif at the level of lips \({\Gamma }_{1}\) and \({\Gamma }_{2}\) of the interface. They are directed from the discontinuity to the massif.

The pressure field at the level of the massif is noted \(p\) and that at the interface level is noted \({p}_{f}\) (field induced by the fluid circulating at the interface level). The movement field is noted \(u\) and the movement jump at the interface level is noted \(⟦u⟧\).

Let \({P}_{1}\) be a point of \({\Gamma }_{1}\) and \({P}_{2}\) a point of \({\Gamma }_{2}\) and \({n}_{c}={n}_{c}^{1}\) be the external normal to \({\Gamma }_{1}\) and \({n}_{c}^{2}\) the external normal to \({\Gamma }_{2}\). The normal displacement jump (taken to be negative or zero when opened and positive when the lips interpenetrate) is therefore defined as follows:

\(⟦u⟧\mathrm{.}{n}_{c}=(u({P}_{1})-u({P}_{2}))\mathrm{.}{n}_{c}⩽0\)

On the, we indicate the conventions adopted to take account of the displacement jump at the interface level.

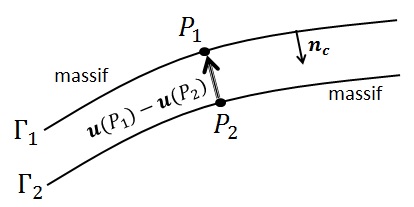
_images/100000000000019E000000CFE02A182774D6F506.jpg

Figure 2.2-2: Definition of the displacement jump at the level of discontinuity

For the massif, as for the interface, the hypothesis of effective constraints is taken into consideration. So:

  • the total stress in the massif is noted \(\sigma\),

  • the total constraint (linked to cohesive efforts) at the interface level is noted \({t}_{c}\).

The hypothesis of small disturbances is accepted. On the other hand, mechanical and hydraulic quantities are considered to be isotropic.