1. Overview of cohesive laws#
In fragile rupture, to overcome the problem of infinite stresses at the bottom of a crack, it is possible to introduce cohesion forces that impose a stress initiation criterion (see (3). The forces are exerted between the particles on both sides of the plane of separation of the crack (see FIG. 1). Historically, one of the first to propose this type of approach was Barenblatt (1) in the early sixties. Based on this idea, numerous models have emerged in the literature under the name: « Cohesive zone models » or CZM in English. For a bibliography you can refer to (5).
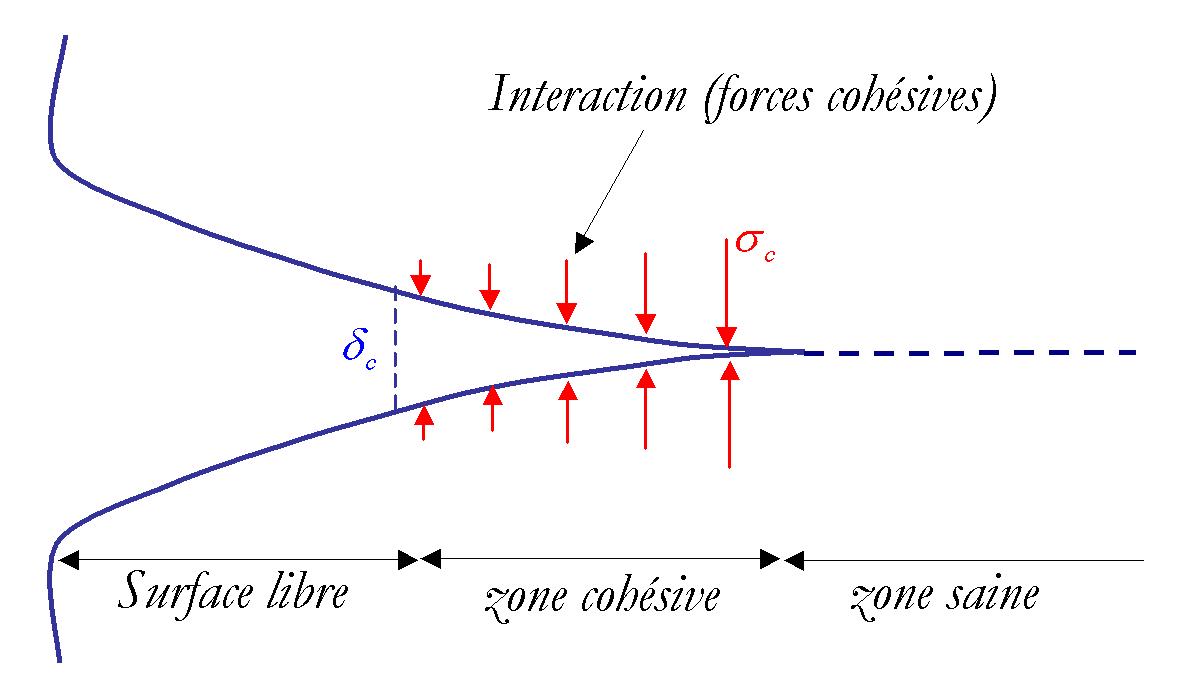
Figure1: Diagram of a crack.
It is considered that the opening of the crack costs energy in proportion to its length. It’s called surface energy, which we note \(\Psi\). The equilibrium displacement field \(u\) is obtained by minimizing the sum of the elastic energy \(\Phi\) of the surface energy \(\mathrm{\Psi }\) and the work of external forces \({W}^{\mathrm{ext.}}\):
\(\underset{u}{\text{min}}(\Phi +\Psi +{W}^{\mathrm{ext}})\)
The discontinuity surface is discretized in 2D or 3D by finite joint elements (see documentation: R3.06.09) or by finite interface elements (in this case the problem is reduced to a search for a saddle point, see R3.06.13). The jump in movement in element \(\delta\) is a linear function of the nodal movements. The force [1] _ The coefficient of cohesion that is exerted on the lips of the crack is noted \(\overrightarrow{\sigma }\), it is defined by the derivative of the surface energy density with respect to the displacement jump.
A relationship between \(\overrightarrow{\sigma }\) and the movement jump \(\delta\) is called cohesive law.
The material parameters of the model are:
the toughness or critical surface energy density noted \({G}_{c}\) (GC keyword) which reflects the energy cost of cracking;
and the critical stress at break noted \({\sigma }_{C}\) (keyword SIGC). In the cohesive laws CZM_xxx_REG presented in the next part, these parameters can depend on a temperature field.
Moreover, the CZM_xxx_REG laws depend on two dimensionless numerical parameters: PENA_ADHERENCE and PENA_CONTACT. The first controls the regulation of surface energy (or penalization of adhesion), the second the penalization of contact.
Laws CZM_xxx_MIX also depend on two numerical parameters PENA_LAGR and RIGI_GLIS. The first is a Lagrangian penalty coefficient and the second determines the stiffness of the sliding (only for law CZM_OUV_MIX). The law dedicated to ductile rupture CZM_TRA_MIX is in the shape of a trapezoid. To define this shape, two additional dimensionless parameters are introduced. They are positive and strictly less than 1, baptized COEF_EXTR as extrinsic [2] _ to determine the slope at the origin (either infinite or not) and COEF_PLAS as plastic to determine the end of the plastic tray.
We will give a detailed definition of the parameters in the parts that follow.
Note:
The following notations are adopted: \(n\) refers to the normal to the crack surface and \(t\) and \(\tau\) the sliding directions in the plane of the crack. For any vector \(\mathrm{x}\) we note:
:math:`begin{array}{}x={x}_{n}n+{x}_{t}t+{x}_{tau }tau ;{langle xrangle }_{text{+}}=langle {x}_{n}rangle n+{x}_{t}t+{x}_{tau }tau ;\ parallel xparallel =sqrt{xcdot x};{parallel xparallel }_{text{+}}=sqrt{{langle xrangle }_{text{+}}cdot {langle xrangle }_{text{+}}}end{array}`*with \({\langle x\rangle }_{i}=\text{sup}({x}_{i},0)\)