2. Definition of cohesive laws CZM_xxx_REG

In this part we present the surface energy \(\Psi\) as well as the resulting stress vector \(\overrightarrow{\sigma }\) for the cohesive laws CZM_EXP_REG and CZM_LIN_REG. The irreversibility of cracking is formulated in the same way for each of them. Moreover, these laws are based on the joint model, which requires the regulation of energy. The latter is carried out by penalizing adhesion.

2.1. Surface energy

Surface energy \(\Psi\), defined on a \(\Gamma\) discontinuity, depends on the jump in displacement between the lips of the crack: \(\delta\) and on \(\kappa\) threshold internal variable that manages the irreversibility of the crack. The latter remembers the highest jump norm reached during the opening. Its law of evolution between two successive loading increments - and + is written as:

\({\kappa }^{\text{+}}=\text{max}({\kappa }^{\text{-}},{\parallel \delta \parallel }_{\text{+}})\)

Surface energy is defined as follows:

\(\psi (\delta ,\kappa )=H({\parallel \delta \parallel }_{\text{+}}-\kappa ){\Psi }_{\mathrm{dis}}({\parallel \delta \parallel }_{\text{+}})+\left[1-H({\parallel \delta \parallel }_{\text{+}}-\kappa )\right]{\Psi }_{\mathrm{lin}}({\parallel \delta \parallel }_{\text{+}},\kappa )+{I}_{{ℝ}_{\text{+}}}({\delta }_{n})\)

with \(H\) Heaviside function and \({I}_{{ℝ}_{\text{+}}}\) indicator function reflecting the condition of non-interpenetration of the crack lips:

\({I}_{{R}^{+}}({\delta }_{n})=\{\begin{array}{c}+\infty \text{si}{\delta }_{n}<0\\ 0\text{si}{\delta }_{n}\ge 0\end{array}\)

Note:

In the standard jump, we take the positive part of the normal jump. This ensures that, when contact is penalized, a negative normal jump cannot contribute to changing the threshold (i.e. dissipating energy) .

Depending on the threshold value, the surface energy will be worth \({\Psi }_{\mathrm{dis}}\) or \({\Psi }_{\mathrm{lin}}\). In the first case we will speak of a dissipative regime (dissipation of energy during cracking), in the second case of linear regime (discharge or linear recharge without energy dissipation). The two forms of energy can be written as follows:

\({\Psi }_{\mathrm{dis}}({\parallel \delta \parallel }_{\text{+}})={\int }_{\Gamma }{\psi }_{\mathrm{dis}}({\parallel \delta \parallel }_{\text{+}})d\Gamma\) and \({\Psi }_{\mathrm{lin}}({\parallel \delta \parallel }_{\text{+}},\kappa )={\int }_{\Gamma }{\psi }_{\mathrm{lin}}({\parallel \delta \parallel }_{\text{+}},\kappa )d\Gamma\)

with \({\Psi }_{\mathrm{dis}}\) and \({\Psi }_{\mathrm{lin}}\) surface energy densities.

Let us present in detail the values of these densities for each cohesive law.

2.1.1. Surface energy density in linear regime

In the case where an existing crack evolves without dissipating energy (i.e. \({\parallel \delta \parallel }_{\text{+}}<\kappa\)), the element is in a linear phase (charge or discharge), the threshold does not evolve. We choose an energy density that is a quadratic function of the jump norm:

(2.1)\[ {\ Psi} _ {\ mathrm {lin}} ({\ parallel\ delta\ parallel}} _ {\ text {+}},\ kappa) =\ frac {1} {2} P (\ kappa) {\ kappa) {\ parallel\ delta\ parallel}} _ {0} _ {0} _ {0} _ {0} _ {0}\]

The \(P\) function depends on the cohesive law:

(2.2)\[ \begin{align}\begin{aligned} \ textrm {**CZM_EXP_REG:**}\\ P (\ kappa) =\ frac {{\ sigma} _ {\ sigma} _ {c}}} {\ kappa}\ text {exp} (-\ frac {{\ sigma} _ {\ sigma} _ {\ sigma}} _ {\ sigma}} _ {c}}\ kappa)\end{aligned}\end{align} \]

(2.3)\[ \begin{align}\begin{aligned} \ textrm {**CZM_LIN_REG:**}\\ P (\ kappa) =\ {\ begin {array} {cc} {\ sigma} {\ sigma} _ {c} (\ frac {1} {\ kappa} -\ frac {{\ sigma} _ {c}}} {2 {G}}} {2 {G} _ {c}}} {2 {G}}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}}} {2 {G} _ {c}} text {si}\ kappa\ ge 2 {G} _ {c} _ {c}/{\ sigma} _ {c}\ end {array}\end{aligned}\end{align} \]

The function \(P\) makes it possible to ensure the continuity of the derivative of \(\Psi\) in \(\kappa\) (i.e. the continuity of the stress vector in the element from one regime to another) and the constant \({C}_{0}\) to ensure the continuity of \(\Psi\) in \(\kappa\).

2.1.2. Surface energy density in a dissipative regime

In the dissipative regime, (case \({\parallel \delta \parallel }_{\text{+}}\ge \kappa\)), a surface energy density of the following form is chosen:

\[\]

: label: eq-4

textrm {CZM_EXP_REG:}

{psi} _ {mathrm {dis}}} ({paralleldeltaparallel}} _ {text {+}}) = {G} _ {x}left [1-text {exp} (-frac {{sigma}} _ {sigma}} _ {sigma}} _ {text {exp}} (-frac {sigma}} _ {sigma}} _ {text {exp}} (-frac {sigma}} _ {sigma}} _ {text {+}})right]

\[\]

: label: eq-5

textrm {CZM_LIN_REG:}

{psi} _ {mathrm {dis}}} ({paralleldeltaparallel}} _ {text {+}}) ={begin {array} {cc}frac {- {sigma} _ {sigma} _ {c}} _ {2}} {c}} {paralleldeltaparallel}} {text {+}}frac {- {sigma} _ {sigma} _ {2} _ {2}} _ {2}} + {sigma}} {c}} {sigma} _ {sigma}} ^ {2}} _ {2}} + {sigma 2}} {c}} {sigma}} _ {c} {paralleldeltaparallel} _ {text {+}} _ {text {+}} &text {si} {paralleldeltaparallel} _ {+}}le 2 {G} _ {c}/{sigma}/{sigma}/{sigma}/{sigma} _ {c} _ {c}ge 2 {G} _ {c}/{sigma} _ {c}end {array}

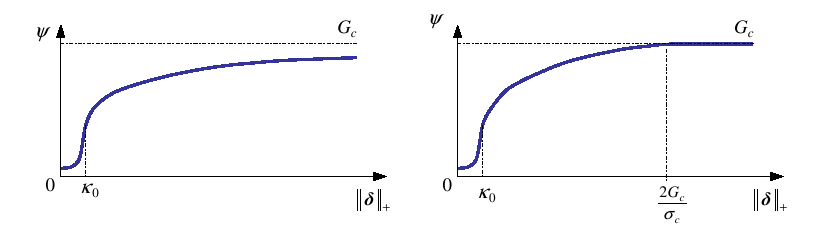
Figure2: Surface energy density as a function of the displacement jump norm, law CZM_EXP_REG on the left and law CZM_LIN_REG on the right.

Surface energy density \({\psi }_{\mathrm{dis}}\) is not differentiable from \(\delta\) at zero. To avoid this problem and maintain a local treatment of the opening conditions, a regularization of this last one is carried out in the vicinity of zero. We consider that the internal variable \(\kappa\) is not zero for a healthy element, let’s note \({\kappa }_{0}\) its initial value. The surface energy at initiation, instead of \(\Psi (\delta ,0)={\Psi }_{\mathrm{dis}}({\parallel \delta \parallel }_{\text{+}})\), will be worth \(\Psi (\delta ,{\kappa }_{0})={\Psi }_{\mathrm{lin}}({\parallel \delta \parallel }_{\text{+}},{\kappa }_{0})\) as long as the jump norm is less than \({\kappa }_{0}\). Surface energy density is shown on Figure 2. This corresponds to a quadratic function of the jump in the vicinity of zero then, beyond \({\kappa }_{0}\), corresponds to the energy density of the dissipative regime.

Regularization introduces an additional parameter into the model. The initial value of the threshold, noted \({\kappa }_{0}\), is defined as follows:

\({\kappa }_{0}=\frac{{G}_{c}}{{\sigma }_{c}}\) PENA_ADHERENCE

where PENA_ADHERENCE is the Code_Aster parameter entered by the user.

Note:

Regularizing the energy to zero makes it possible to define a stress in the priming joint element. Physically, this means that as soon as the constraint will**increase, a small jump will appear. The softening behavior will only take place when the norm of the jump in the element exceeds *:math:`{kappa }_{0}`, before the joint behaves like a spring. *

2.1.3. Penalization surface energy density

The indicator reflects the condition of non-interpenetration of the crack lips. It is approximated numerically by a continuous \({\Psi }_{\mathrm{pen}}\) penalty function that « rapidly » tends to infinity when the normal jump becomes negative. Thus, the minimization of energy excludes cases where the edges of the joint tend to interpenetrate significantly. We choose:

(2.4)\[ {I} _ {{328} _ {\ text {+}}} (\ delta\ cdot n) = {\ psi} _ {\ mathrm {pen}} (\ delta\ cdot n) =\ frac {1} {2} {2} C {\ langle\ delta\ cdot n\ rangle} _ {\ langle\ delta\ cdot n\ rangle} _ {0} _ {0}\]

with \(C\) constant defined in paragraph 2.2.3 and \({C}_{0}\) arbitrary constant that is not involved in the writing of the cohesive law (see next part).

2.2. Constraint vector

The stress vector in the element noted \(\overrightarrow{\sigma }\) is equal to the sum of the derivatives of the surface energy density and the penalization energy density with respect to the jump.

(2.5)\[ \ overrightarrow {\ sigma} =H ({\ parallel\ delta\ parallel} _ {\ text {+}} -\ kappa) {\ overrightarrow {\ sigma}} _ {\ mathrm {dis}}} +\ left [}} +\ left [1-H ({\ parallel\ delta\ parallel}} _ {\ text {+}}} -\ kappa)\ right] {\ mathrm {dis}}} +\ left [1-H ({\ parallel\ delta\ parallel}} _ {\ text {+}}} -\ kappa)\ right] {\ mathrm {dis}}} +\ left [1-H ({\ parallel\ delta\ parallel}} _ {\ text {+}}} -\ kappa)\ right] {\ mathrm {dis}}}}} _ {\ mathrm {lin}}} + {\ overrightarrow {\ sigma}} _ {\ mathrm {pen}}\]

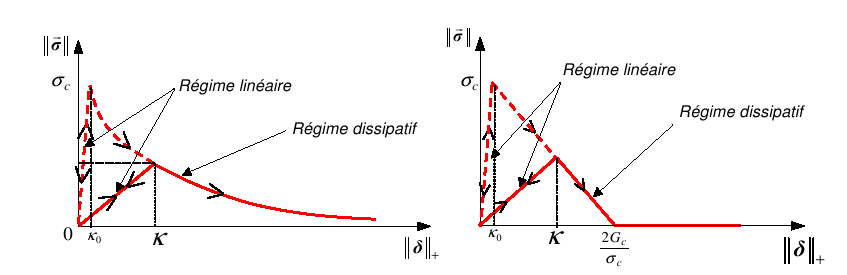
Figure3: Norm of the stress vector according to the norm of the jump, law CZM_EXP_REG on the left, law CZM_LIN_REG on the right.

The norm of the stress vector is represented as a function of the norm of the jump in FIG. 3. The arrows represent the possible direction of evolution of the constraint depending on whether the opening process is reversible (linear regime) or not (dissipative regime). At initiation, the element behaves linearly with a significant slope (regularization), then at a softening behavior. The slope at zero is governed by the initial value of threshold \({\kappa }_{0}\).

2.2.1. Constrained vector in linear regime

The stress vector in linear regime is written (see figure 3):

(2.6)\[ {\ overrightarrow {\ sigma}} _ {\ mathrm {lin}}} =\ frac {\ partial {\ psi} _ {\ mathrm {lin}}}} {\ partial\ delta}} {\ partial\ delta} =P (\ kappa)\ delta\]

and the tangent module:

(2.7)\[\begin{split} \ frac {\ partial {\ overrightarrow {\ sigma}}} _ {\ mathrm {lin}}} {\ partial\ delta} =P (\ kappa) (\ begin {array} {cc} {cc} H (\ delta\ cdot n) & 0\\ 0& 1\ end {array})\end{split}\]

with

defined by () or () according to the cohesive law.

2.2.2. Constrained vector in dissipative regime

The stress vector in the dissipative regime is written (see figure 3):

(2.8)\[ \begin{align}\begin{aligned} \ textrm {**CZM_EXP_REG:**}\\ {\ overrightarrow {\ sigma}} _ {\ mathrm {dis}}} =\ frac {\ partial {\ psi} _ {\ mathrm {dis}}} {\ partial\ delta} = {\ sigma} = {\ sigma} _ {c} _ {c}}\ frac {\ frac {\ delta}}}\ mathrm {exp} _ {\ text {+}}}\ mathrm {exp} (\ frac {- {\ sigma} _ {c}} {{G}} {{G} _ {c}} {\ parallel\ delta\ parallel} _ {\ text {+}}})\end{aligned}\end{align} \]

(2.9)\[ \begin{align}\begin{aligned} \ textrm {**CZM_LIN_REG:**}\\ {\ overrightarrow {\ sigma}} _ {\ mathrm {dis}}} =\ frac {\ partial {\ psi} _ {\ mathrm {dis}}} {\ partial\ delta} =\ {\ begin {array} {array} {\ array} {{array} {{array} {{array} {cc} {cc} {\ sigma}} _ {\ text {+}}} -\ frac {{\ sigma} _ {c}} {2 {G}}} {2 {G} _ {c}}) &\ text {si} {\ parallel\ delta\ parallel} _ {+}}\ le 2 {G} _ {c} _ {c}}/{c}/{\ sigma}/{c} _ {\ sigma} _ {\ text {+}} _ {c}/{\ sigma} _ {c}/{\ sigma} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c} _ {c}} _ {c} _ {c} _ {c} _ {c} _ {c}}\ ge 2 G} _ {c}/{\ sigma} _ {c}\ end {array}\end{aligned}\end{align} \]

and the tangent module:

(2.10)\[ \begin{align}\begin{aligned} \ textrm {**CZM_EXP_REG:**}\\ \ frac {\ partial {\ overrightarrow {\ sigma}}} _ {\ mathrm {dis}}} {\ partial\ delta} = {\ sigma} _ {c}\ left [\ frac {\ mathrm {Id}} {\ frac {\ mathrm {Id}}}} {{\ parallel\ mathrm {Id}}} {{\ parallel\ delta {Id}}} {{\ parallel\ delta {Id}}} {{\ parallel\ delta\ parallel}} _ {\ text {+}}}\ otimes\ frac {\ delta} {{\ parallel\ delta\ parallel} _ {\ text {+}}}} (\ frac {{\ sigma} _ {c}}} {{G}} _ {c}}} +\ frac {\ c}}} +\ frac {1} {\ parallel\ delta\ parallel\ parallel}} _ {\ text {+}}})\ right]\ mathrm {exp}})\ right]\ mathrm {exp}} (\ frac {- {\ sigma} _ {c}}} {{c}} {{G}} {\ parallel\ delta\ parallel} _ {\ text {+}}})\end{aligned}\end{align} \]

(2.11)\[ \begin{align}\begin{aligned} \ textrm {**CZM_LIN_REG:**}\\\begin{split} \ frac {\ partial {\ overrightarrow {\ sigma}}} _ {\ mathrm {dis}}} {\ partial\ delta} =\ {\ begin {array} {cc}\ frac {{\ sigma} _ {c} _ {c}}} {{\ parallel\ sigma} _ {c}}} {\ parallel\ delta\ parallel}}}}\ left [(1-\ frac {{\ sigma}} _ {c}}}\ left [(1-\ frac {{\ sigma}} _ {c}}} {2 {G} _ {c}} {\ parallel\ delta\ parallel}} _ {\ text {+}})\ mathrm {Id} -\ frac {\ delta} {{\ parallel\ delta\ parallel}} _ {\ text {+}} _ {\ text {+}} _ {\ text {+}}} _ {\ text {+}}} _ {\ text {+}}} _ {\ text {+}} _ {\ text {+}}} _ {\ text {+}}} _ {\ text {+}} _ {\ text {+}}} _ {\ text {+}} _ {\ text {+}}} _ {\ text {+}}} _ {\ text {+}}} _ {\ text {+}}}\ right] {+}} If} {\ parallel\ delta\ parallel} _ {\ text {+}}\ le\ frac {2 {G} _ {c}} {{\ sigma} _ {c}}\\ 0&\ text {si} {\ text {si} {\ parallel\ delta\ parallel} {\ text {+}}\ le\ frac {2 {G}}} {{\ sigma}}} {{\ sigma}} {si} {\ sigma} {}} {\ sigma} {}} {\ sigma} {}} {\ sigma} {\ sigma} {}} {\ sigma} {\ sigma} {}} {\ sigma} {{c}} {\ sigma} {\ sigma} {}} {\ sigma} {}} {\ sigma} {\ sigma} {}} {\ sigma} {\ sigma} {{array}\end{split}\end{aligned}\end{align} \]

2.2.3. Constraint vector of penalization

The penalization stress vector is written as:

(2.12)\[ {\ overrightarrow {\ sigma}} _ {\ mathrm {pen}}} =\ frac {\ partial {\ psi} _ {\ mathrm {pen}}} {\ partial\ delta} =C (\ begin {array} =C (\ begin {array} {} {\ array} {} {\ array}} {\ begin {array}} =C (\ begin {array}} {\ array}} =C (\ begin {array}} {\ array} {}} {\ begin {array}} {\ array} {}} {\ begin {array} {} {\ array}} {\ begin {array} {}} {\ begin {array} {} {\ array} {}} {\ begin {array}} {} {\ array} {\]

and the tangent module:

(2.13)\[\begin{split} \ frac {\ partial {\ overrightarrow {\ sigma}}} _ {\ mathrm {pen}}} {\ partial\ delta} =C (\ begin {array} {cc} H (-\ delta\ cdot n) & 0\\ 0& 0\ end {array})\end{split}\]

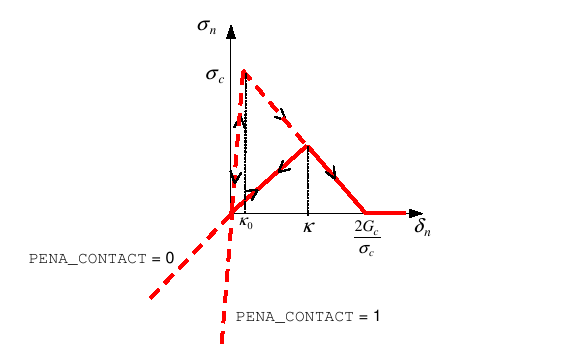
Figure4: Normal cohesive stress as a function of the normal jump (case of an opening in pure I mode)

The value of the penalty slope

is given by the relationship:

(2.14)\[ C=P (\ kappa) +\]

with \(P\) defined by () or () according to the cohesive law. The numerical parameter PENA_CONTACT, entered by the user, makes it possible to play on the slope of the contact penalty (see figure 4). The latter value by default is 1, this corresponds to the case where the slope of the contact is identical to that of the initial adhesion. If you choose a value greater than 1, you increase the penalty. If 0 is chosen, the penalty is identical to the slope of the current elastic discharge.

2.3. Internal variables

Laws CZM_EXP_REG and CZM_LIN_REG each have nine internal variables. From the point of view of the law of behavior, only the former is*stricto sensu* an internal variable. The others provide information on the condition of the joint at a given moment.

Internal variables identical for both laws:

\(\mathrm{V1}=\kappa\): jump threshold (highest norm reached).

\(\mathrm{V2}\): dissipation indicator \(=0\) if linear regime, \(=1\) if dissipative regime.

\(\mathrm{V5}=\mathrm{V4}\times {G}_{c}\): value of the energy dissipated (see figure 5).

\(\mathrm{V7}={\delta }_{n}\): normal jump, \(\mathrm{V8}={\delta }_{t}\) tangential jump, \(\mathrm{V9}={\delta }_{\tau }\) tangential jump (null in 2D).

Internal variables for CZM_EXP_REG :

\(\mathrm{V3}\): damage indicator \(=0\) if healthy material (\(\kappa ={\kappa }_{0}\)) \(=1\), if damaged material (\(\kappa >{\kappa }_{0}\)),

\(\mathrm{V4}=1-(1+\frac{{\sigma }_{c}}{2{G}_{c}}\kappa )\mathrm{exp}(\frac{-{\sigma }_{c}}{{G}_{c}}\kappa )\): percentage of energy dissipated.

\(\mathrm{V6}=\frac{1}{2}{\parallel \delta \parallel }_{\text{+}}^{2}\frac{{\sigma }_{c}}{\kappa }\mathrm{exp}(\frac{-{\sigma }_{c}}{{G}_{c}}\kappa )\): current residual energy value.

Internal variables for CZM_LIN_REG :

\({v}_{3}\): damage indicator \(=0\) if healthy material (\(\kappa ={\kappa }_{0}\)) \(=1\), if damaged material (\({\kappa }_{0}<\kappa <2{G}_{c}/{\sigma }_{c}\)),

if material is broken (\(\kappa \ge 2{G}_{c}/{\sigma }_{c}\)).

: percentage of energy dissipated.

\(\mathrm{V6}=\frac{1}{2}{\parallel \delta \parallel }_{\text{+}}^{2}{\sigma }_{c}(\frac{1}{\kappa }-\frac{{\sigma }_{c}}{2{G}_{c}})\): current residual energy value (see figure 5).

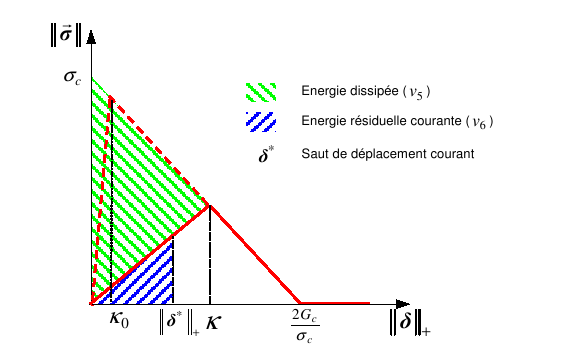
Figure5: Representation of energies for the law. CZM_LIN_REG .

Note:

We have seen that for the purposes of energy regulation, the initial threshold \({\kappa }_{0}\) (threshold for a healthy element) is not zero. This therefore implies that the energy dissipated (internal variable \(\mathrm{V5}\) ) is not zero for a healthy element. This has no physical reality, this internal variable only has meaning once the initial threshold is crossed: \(\kappa >{\kappa }_{0}\) .