3. Definition of cohesive laws CZM_xxx_MIX#
These laws are intended to:
to the modeling of an elastic interface or to the elementary verification of the data set of a cracking problem with law CZM_ELAS_MIX;
at the fragile or almost fragile break (monotonic loading) for CZM_OUV_MIX, CZM_TAC_MIX, and CZM_EXP_MIX. The exponential form of law CZM_EXP_MIX is well suited to represent concrete breakage.
at the ductile break for CZM_TRA_MIX,
to fatigue (cyclic loading) for CZM_FAT_MIX,
to the degradation of a steel-concrete interface for CZM_LAB_MIX.
In this part we present the surface energy \(\Psi\) as well as the stress vector \(\overrightarrow{\sigma }\) for each of them, then the numerical parameters and the internal variables. The irreversibility of cracking is formulated in the same way for the first four laws and CZM_LAB_MIX (of the Talon-Curnier type with vertical discharge (6)) For CZM_FAT_MIX, it is based on the accumulation of openness during the cycles.
The mixed Augmented Lagrangian formulation makes it possible to avoid the regulation of surface energy. This makes it possible to model the perfect adherence of the interface in a healthy state. For more information on the interface model (*_ INTERFACE and*_ INTERFACE_S), the reader can refer to the R3.06.13 documentation.
3.1. Elastic cohesive law CZM_ELAS_MIX#
The reader will be able to find the details of the formulation and numerical implementation of this model in document (10). Only the main results are provided here, using the notations introduced in [R3.06.13]. The mechanical characteristics of the model are specified in command DEFI_MATERIAU (U4.43.01) under the keyword CZM_ELAS.
3.1.1. Surface energy#
The surface energy \(\Psi\), defined on a discontinuity \(\Gamma\), depends quadratically on the displacement jump \(\mathrm{\delta }\) between the lips of the crack:
with surface energy density:
\(\mathrm{\Pi }(\mathrm{\delta })=\mathrm{\psi }(\mathrm{\delta })+{A}_{n}({\delta }_{n})+{A}_{t}({\delta }_{t},{\delta }_{\tau })\)
Function \(\mathrm{\psi }\) refers to elastic energy density:
\(\mathrm{\psi }(\mathrm{\delta })=\frac{1}{2}{k}_{\mathit{nt}}{⟨{\delta }_{n}⟩}_{\text{+}}^{2}+\frac{1}{2}{k}_{\mathit{nc}}{⟨{\delta }_{n}⟩}_{\text{-}}^{2}+\frac{1}{2}{k}_{t}({\delta }_{t}^{2}+{\delta }_{\tau }^{2})\)
where \({k}_{\mathit{nt}}\), \({k}_{\mathit{nc}}\) and \({k}_{t}\) respectively designate the modules of normal tensile stiffness, normal compressive stiffness, and tangential stiffness. In command DEFI_MATERIAU, they are entered under the keywords RIG_NOR_TRAC, RIGI_NOR_COMP, and RIG_TAN respectively. When \({k}_{\mathit{nt}}={k}_{\mathit{nc}}\), the stiffness is identical in tension and compression and can be specified by a single RIG_NOR keyword.
The \({A}_{t}\) function makes it possible to consider a perfectly adherent or elastic tangential behavior:
\({\mathrm{A}}_{\mathrm{t}}({\delta }_{t},{\delta }_{\tau })=\{\begin{array}{cc}{I}_{\text{{ (0,0) }}}(({\delta }_{t},{\delta }_{\tau }))& \text{en adhérence parfaite}\\ 0& \text{en élasticité}\end{array}\)
The choice between perfect grip and elasticity for the tangent direction is determined by the ADHE_TAN keyword in DEFI_MATERIAU (“PARFAITE” or “ELAS”). Recall that an indicator function \({I}_{K}(x)\) is defined as follows:
\({I}_{K}(x)=\{\begin{array}{c}+\mathrm{\infty }\text{si}x\notin K\\ 0\text{si}x\in K\end{array}\)
Finally, function \({A}_{n}\) makes it possible to consider normal behavior that is perfectly adherent, with a condition of unilateral contact (and elasticity when opening) or elastic when opening and closing:
\({\mathrm{A}}_{\mathrm{n}}({\mathrm{\delta }}_{\mathrm{n}})=\{\begin{array}{cc}{I}_{\text{{ 0 }}}({\mathrm{\delta }}_{\mathrm{n}})& \text{en adhérence parfaite}\\ {I}_{{\mathrm{ℝ}}^{\text{+}}}({\mathrm{\delta }}_{\mathrm{n}})& \text{en contact unilatéral}\\ 0& \text{en élasticité}\end{array}\)
The choice between perfect grip, one-sided contact, and elasticity for the normal direction is determined by the ADHE_NOR keyword from DEFI_MATERIAU (“PARFAITE”, “UNILATER”, or “ELAS”).
3.1.2. Constraint vector#
The stress vector \(\vec{\mathrm{\sigma }}\) derives from surface energy \(\mathrm{\Pi }\). But in the presence of adhesion or contact conditions, the latter is not derivable at all points. The concept of derivative is then generalized by that of sub-differential. Without going into details, the following relationships between the stress vector and the displacement jump follow:
For normal behavior:
\(\{\begin{array}{cc}\text{adhérence parfaite}& {\delta }_{n}=0\text{et}{\sigma }_{n}\text{quelconque}\\ \text{contact unilatéral}& {\delta }_{n}=\frac{1}{{k}_{\mathit{nt}}}⟨{\sigma }_{n}⟩\\ \text{élasticité}& {\delta }_{n}=\frac{1}{{k}_{\mathit{nt}}}{⟨{\sigma }_{n}⟩}_{\text{+}}+\frac{1}{{k}_{\mathit{nc}}}{⟨{\sigma }_{n}⟩}_{\text{-}}\end{array}\)
And for tangential behavior:
\(\{\begin{array}{cc}\text{adhérence parfaite}& {\delta }_{t}={\delta }_{\tau }=0\text{et}({\sigma }_{t},{\sigma }_{\tau })\text{quelconque}\\ \text{élasticité}& {\delta }_{t}=\frac{1}{{k}_{t}}{\sigma }_{t}\text{et}{\delta }_{\tau }=\frac{1}{{k}_{t}}{\sigma }_{\tau }\end{array}\)
3.1.3. Augmented Lagrangian and behavioral relationship integration#
In accordance with [R3.06.13], the Lagrangian of the relaxed interface problem is increased by a penalty term where \(r\) refers to the increase coefficient. The value of \(r\) is set by the user under the PENA_LAGR_ABSO keyword, with the unit being a constraint per unit area (\(J/{m}^{4}\)).
Integrating the mixed behavior relationship consists in solving the following algebraic system:
\(\lambda +r(⟦u⟧-\delta )\in \partial \mathrm{\Pi }(\delta )\)
where \(\lambda\) refers to the Lagrange multiplier (the increased nodal cohesive force), \(⟦u⟧\) is the displacement jump calculated from the nodal displacements and \(\delta\) is the local displacement jump (at the integration points), the result of the process of integrating the law of behavior. At this point, \(\lambda\) and \(⟦u⟧\) are known quantities and \(\delta\) is the unknown to the system.
Noting \(\varphi \equiv \lambda +r⟦u⟧\), the solution to the algebraic system is as follows, based on the results of (10):
Normal behavior:
\(\{\begin{array}{cc}\text{adhérence parfaite}& {\delta }_{n}=0\\ \text{contact unilatéral}& {\delta }_{n}=\frac{1}{{k}_{\mathit{nt}}+r}⟨{\varphi }_{n}⟩\\ \text{élasticité}& {\delta }_{n}=\frac{1}{{k}_{n}+r}{\varphi }_{n}\text{avec}{k}_{n}={k}_{\mathit{nt}}\text{si}{\varphi }_{n}>0\text{et}{k}_{n}={k}_{\mathit{nc}}\text{si}{\varphi }_{n}\le 0\end{array}\)
And for tangential behavior:
\(\{\begin{array}{cc}\text{adhérence parfaite}& {\delta }_{t}={\delta }_{\tau }=0\\ \text{élasticité}& {\delta }_{t}=\frac{1}{{k}_{t}+r}{\varphi }_{t}\text{et}{\delta }_{\tau }=\frac{1}{{k}_{t}+r}{\varphi }_{\tau }\end{array}\)
3.1.4. Internal variables#
Since interface behavior is elastic, there are no internal variables in the strict sense. On the other hand, the local displacement jump \(\delta\) is provided for post-processing purposes. Its components \(({\delta }_{n},{\delta }_{t},{\delta }_{\tau })\) are listed in the table of internal variables (V1, V2, V3).
3.2. Cohesive laws for fragile breakup CZM_OUV_MIX, CZM_TAC_MIX, and CZM_EXP_MIX#
3.2.1. Surface energy#
Surface energy \(\Psi\), defined on a \(\Gamma\) discontinuity, depends on the jump in displacement between the lips of the crack: \(\delta\) and on \(\kappa\) threshold internal variable that manages the irreversibility of the crack. The latter remembers the highest jump norm reached during the opening. Its law of evolution between two successive loading increments - and + is written as:
\({\kappa }^{\text{+}}=\text{max}({\kappa }^{\text{-}},\parallel \delta \parallel )\)
Surface energy is defined as follows:
with surface energy density:
\(\Pi (\delta ,\kappa )=\psi (\text{max}(\parallel \delta \parallel ,\kappa ))+{I}_{{ℝ}^{\text{+}}}({\delta }_{n})\)
where \({I}_{{ℝ}^{\text{+}}}\) indicator function translating the condition of non-interpenetration of the lips of the crack:
\({I}_{{ℝ}^{\text{+}}}({\delta }_{n})=\{\begin{array}{}+\infty \text{si}{\delta }_{n}<0\\ 0\text{si}{\delta }_{n}\ge 0\end{array}\)
and \(\psi\) cohesive energy density defined as follows:
: label: eq-20
textrm {CZM_OUV_MIX:}
begin {array} {c}psi ({delta} _ {n}) ={begin {array} {cc}frac {- {sigma} _ {c} ^ {2}} {4 {G}} {4 {G} _ {c} _ {c}} _ {c} _ {2} + {sigma} _ {c} {delta} _ {2}} {delta} _ {2}} {4 {G} _ {2}} {4 {G} _ {G} _ {2}} {4 {G} _ {g} _ {2}} {4 {G} _ {g} _ {g} _ {g} _ {g} _ {c} _ {2}} {4 {G} _ {g} _ {g} _ {g} _ {delta} _ {n}le 2 {G} _ {c} _ {c}/{sigma} _ {c} _ {c} &text {delta} _ {n}ge 2 {G} _ {g} _ {c}} _ {c}/{c}/{sigma} _ {sigma} _ {G} _ {T}) =frac {1} {T}) =frac {1} {T}) 2} C {delta} _ {T} ^ {2} T=ttext {or}tauend {array}
Notes:
:math:`C`*depends on a numerical parameter chosen by the user (see part:ref:`3.5 <Ref207599345>`*) *
For the law CZM_OUV_MIX the dissipation is only controlled by the normal opening, the evolution of the threshold is therefore strictly defined as follows: \({\kappa }^{\text{+}}=\text{max}({\kappa }^{\text{-}},{\delta }_{n})\)
Since the length of the cohesive zone is longer for the law CZM_EXP_MIX than for the other CZM interface laws, an increase in the number of cells or the penalty coefficient is necessary to obtain a solution.
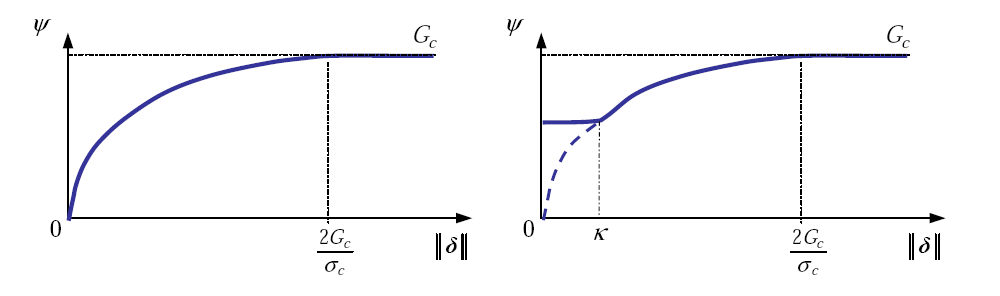
Figure6 : Surface energy density as a function of the displacement jump norm, law CZM_TAC_MIX.
Law CZM_OUV_MIX has a softening behavior when opened and « elastic » in sliding mode while CZM_TAC_MIX (figure 6) couples softening in the three break modes. The first only models energy dissipation in mode I. It is intended for the particular case of modeling in pure opening mode for which it is desired to impose a symmetry condition on the lips of the cohesive finite elements that carry it (interface elements). The second is valid in other cases.
3.2.2. Constraint vector#
The surface energy defined above cannot be derived in the following cases: \(\delta =0\) (perfect adhesion before initiating), \({\delta }_{n}=0\) (contact) and \(\parallel \delta \parallel =\kappa\) (vertical discharge of the Talon-Curnier type). The stress vector noted \(\overrightarrow{\sigma }\) is then defined as belonging to the subdifferential (generalization of the concept of derivative) of the surface energy density.
+———————————————————-++ |:math:`\overrightarrow{\sigma }\in \partial \Pi (\delta )`|| +———————————————————-++
This set coincides with the derivative at the points where it is differentiable and with a set of possible directional derivatives otherwise. For more details, refer to the interface elements doc R7.02.13. Let us give here the values taken by this set in the various cases for law CZM_TAC_MIX:
Perfect adhesion before priming (\(\kappa =0\) and \(\delta =0\)):
\(\partial \Pi (\delta )=\{x\in {ℝ}^{3};{\parallel x\parallel }_{\text{+}}\le {\sigma }_{c}\}\)
Charge/Discharge back to zero (\(\parallel \delta \parallel <\kappa\)) and contact condition:
\(\partial \Pi (\delta )=\{{x}_{n}n;{x}_{n}\le 0\text{et}{\delta }_{n}\ge 0\text{et}{x}_{n}{\delta }_{n}=0\}\)
Vertical Charge/Discharge (\(\parallel \delta \parallel =\kappa >0\)) and contact condition:
\(\partial \Pi (\delta )=\{{x}_{n}n+\lambda \delta ;0\le \lambda \le \frac{\psi \text{'}(\kappa )}{\kappa }\text{et}{x}_{n}\le 0\text{et}{\delta }_{n}\ge 0\text{et}{x}_{n}{\delta }_{n}=0\}\)
Damage, breakage (\(\parallel \delta \parallel >\kappa\)) and contact condition:
\(\partial \Pi (\delta )=\{{x}_{n}n+\frac{\psi \text{'}(\parallel \delta \parallel )}{\parallel \delta \parallel }\delta ;{x}_{n}\le 0\text{et}{\delta }_{n}\ge 0\text{et}{x}_{n}{\delta }_{n}=0\}\)
For the law CZM_OUV_MIXe and the law CZM_EXP_MIX, the modes are decoupled, we can explain the subdifferentials (sets of scalars) in the following form:
Mode I:
Adhesion before priming (\(\kappa =0\) and \({\delta }_{n}=0\)):
\(\partial \Pi ({\delta }_{n})=\{{x}_{n}\in ℝ;{x}_{n}\le {\sigma }_{c}\}\)
Charge/Discharge back to zero (\({\delta }_{n}<\kappa\)) and contact condition:
\(\partial \Pi ({\delta }_{n})=\{{x}_{n};{x}_{n}\le 0\text{et}{\delta }_{n}\ge 0\text{et}{x}_{n}{\delta }_{n}=0\}\)
Vertical Charge/Discharge (\({\delta }_{n}=\kappa >0\)):
\(\partial \Pi ({\delta }_{n})=\{\lambda {\delta }_{n};0\le \lambda \le \frac{\psi \text{'}(\kappa )}{\kappa }\}\)
Damage and breakage (\({\delta }_{n}>\kappa\)):
\(\partial \Pi ({\delta }_{n})=\{\psi \text{'}({\delta }_{n})\}\)
Mode II or III :
Elastic behavior:
\(\partial \Pi ({\delta }_{T})=\{\psi \text{'}({\delta }_{T})\}\text{, T =}t\text{ou}\tau\)
The two laws are detailed here using a more usual form of writing.
Law CZM_OUV_MIX:
\({\sigma }_{n}\{\begin{array}{cc}=\{\begin{array}{c}{\sigma }_{c}\left(1-{\delta }_{n}\frac{{\sigma }_{c}}{2{\%}_{c}}\right)\\ 0\end{array}& \begin{array}{c}\text{si}\kappa <{\delta }_{n}\le 2{\%}_{c}/{\sigma }_{c}\text{( endommagement )}\\ \\ \text{si}{\delta }_{n}>2{\%}_{c}/{\sigma }_{c}\text{(rupture ) ou}0<{\delta }_{n}<\kappa \text{(retour à zéro)}\end{array}\\ \in ]-\infty ,{\sigma }_{c}]& \text{si}{\delta }_{n}=0\text{et}\kappa =0\text{( adhésion et contact )}\\ \in ]-\infty ,0]& \text{si}{\delta }_{n}=0\text{et}\kappa >0\text{( contact )}\\ \in ]\mathrm{0,}{\sigma }_{c}\left(1-\kappa \frac{{\sigma }_{c}}{2{G}_{c}}\right)]& \text{si}{\delta }_{n}=\kappa \text{( charge / décharge verticale )}\end{array}\)
\({\sigma }_{T}=C{\delta }_{T}\text{où}T=t\text{ou}\tau \text{( comportement élastique)}\) (see 3.5 for the definition of \(C\))
A graphical representation is given in FIG. 7.
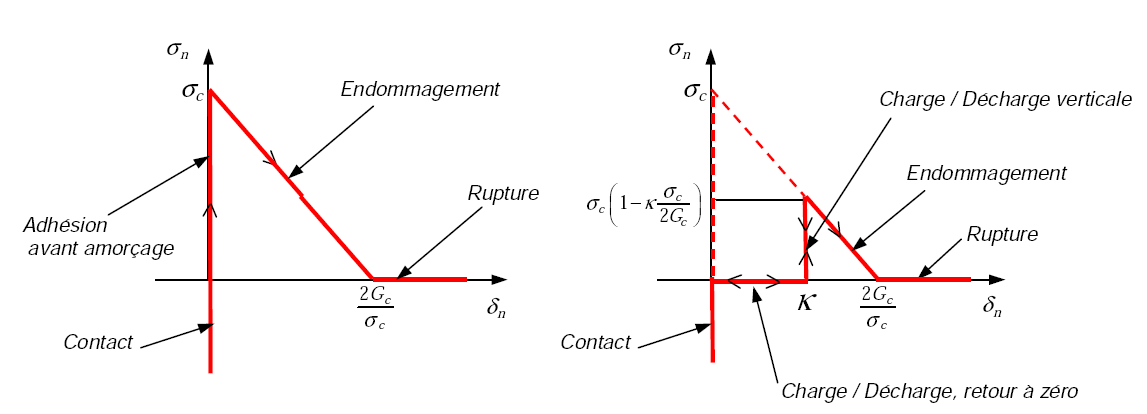
Figure7: Normal component of the stress vector as a function of the normal jump for the law CZM_OUV_MIX (threshold \(\kappa\) zero on the left and positive on the right).
Law CZM_EXP_MIX
\({\sigma }_{n}\{\begin{array}{cc}=\{\begin{array}{c}{\sigma }_{c}\mathrm{exp}(-{\delta }_{n}\frac{{\sigma }_{c}}{{G}_{c}})\\ 0\end{array}& \begin{array}{c}\text{si}\kappa <{\delta }_{n}\le 3.2{G}_{c}/{\sigma }_{c}\text{( endommagement )}\\ \\ \text{si}{\delta }_{n}>3.2{G}_{c}/{\sigma }_{c}\text{(rupture ) ou}0<{\delta }_{n}<\kappa \text{(retour à zéro)}\end{array}\\ \in ]-\infty ,{\sigma }_{c}]& \text{si}{\delta }_{n}=0\text{et}\kappa =0\text{( adhésion et contact )}\\ \in ]-\infty ,0]& \text{si}{\delta }_{n}=0\text{et}\kappa >0\text{( contact )}\\ \in ]\mathrm{0,}{\sigma }_{c}\mathrm{exp}(-\kappa \frac{{\sigma }_{c}}{{G}_{c}})]& \text{si}{\delta }_{n}=\kappa \text{( charge / décharge verticale )}\end{array}\)
\({\sigma }_{T}=C{\delta }_{T}\text{où}T=t\text{ou}\tau \text{( comportement élastique)}\) (see 3.5 for the definition of \(C\))
A graphical representation is given in FIG. 8.
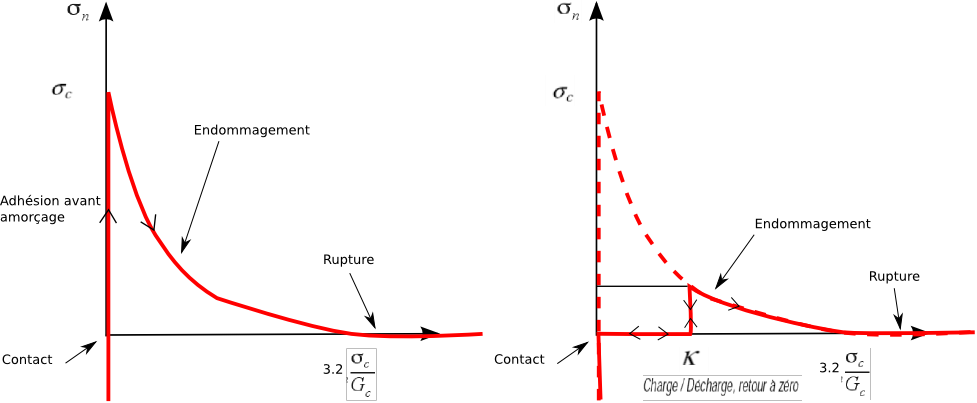
Figure 8: Normal component of the stress vector as a function of the normal jump for law CZM_EXP_MIX (threshold \(\kappa\) zero on the left and positive on the right).
In cases where energy is differentiable, the tangent modulus is easy to determine. Let us give the value of the latter for the phases of damage and rupture:
CZM_TAC_MIX: \(\frac{\partial \vec{\sigma }}{\partial \delta }=\{\begin{array}{cc}\frac{{\sigma }_{c}}{\parallel \delta \parallel }\left[\left(1-\frac{{\sigma }_{c}}{2{\%}_{c}}\parallel \delta \parallel \right)\mathrm{Id}-\frac{\delta }{\parallel \delta \parallel }\otimes \frac{\delta }{\parallel \delta \parallel }\right]& \text{si}{\parallel \delta \parallel }_{\text{+}}\le 2{\%}_{c}/{\sigma }_{c}\\ 0& \text{si}\parallel \delta \parallel \ge 2{\%}_{c}/{\sigma }_{c}\end{array}\)
CZM_OUV_MIX: \(\frac{\partial {\sigma }_{n}}{\partial {\delta }_{n}}=\{\begin{array}{cc}-{\sigma }_{c}^{2}/2{\%}_{c}& \text{si}{\delta }_{n}\le 2{\%}_{c}/{\sigma }_{c}\\ 0& \text{si}{\delta }_{n}\ge 2{\%}_{c}/{\sigma }_{c}\end{array}\)
CZM_EXP_MIX: \(\frac{\partial {\sigma }_{n}}{\partial {\delta }_{n}}=\{\begin{array}{cc}-{\sigma }_{c}^{2}/{G}_{c}\mathrm{exp}(-{\delta }_{n}\frac{{\sigma }_{c}}{{G}_{c}})& \text{si}{\delta }_{n}\le 3.2{G}_{c}/{\sigma }_{c}\\ 0& \text{si}{\delta }_{n}\ge 3.2{G}_{c}/{\sigma }_{c}\end{array}\)
3.3. Cohesive law for ductile rupture CZM_TRA_MIX#
3.3.1. Surface energy#
Surface energy \(\Psi\), defined on a \(\Gamma\) discontinuity, depends on the jump in displacement between the lips of the crack: \(\delta\) and on \(\kappa\) threshold internal variable that manages the irreversibility of the crack. The latter stores the largest normal jump value reached during loading. We will give more details about its evolution in the next part. Surface energy is defined as follows:
with surface energy density:
\(\Pi (\delta ,\kappa )\mathrm{=}\psi (\text{max}({\delta }_{n},\kappa ))+{I}_{{\mathrm{ℝ}}^{\text{+}}}({\delta }_{n})\)
where \({I}_{{ℝ}^{\text{+}}}\) indicator function translating the condition of non-interpenetration of the lips of the crack:
\({I}_{{\mathrm{ℝ}}^{\text{+}}}({\delta }_{n})\mathrm{=}\mathrm{\{}\begin{array}{c}+\mathrm{\infty }\text{si}{\delta }_{n}<{\delta }_{\mathit{res}}\\ 0\text{si}{\delta }_{n}\mathrm{\ge }{\delta }_{\mathit{res}}\end{array}\) with \({\delta }_{\mathrm{res}}\) residual contact jump defined in part 3.3.2.
In case the cracking has not evolved [3] _ 3.3.2 (healthy material), the residual contact jump is zero and \(\psi\) the cohesive energy density is defined as follows:
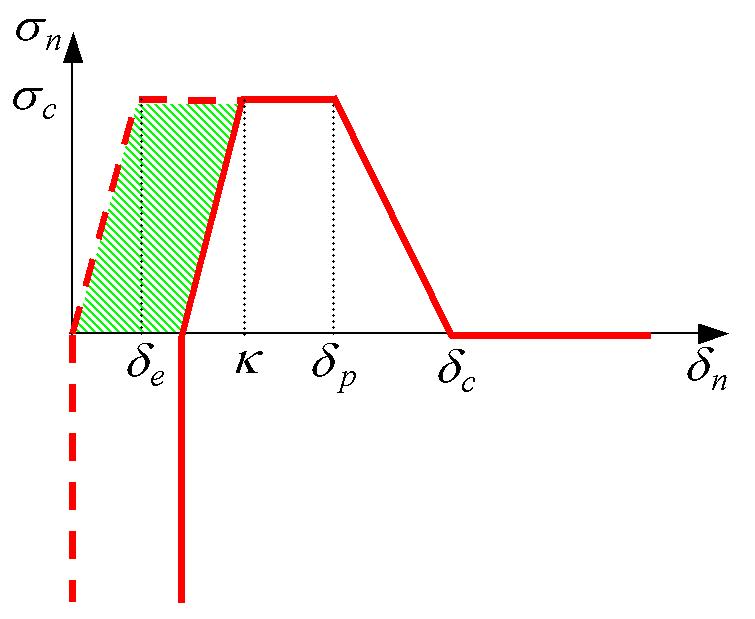
Critical jump \({\delta }_{c}\) is deduced from the other parameters in the following way: \({\delta }_{c}={\mathrm{2G}}_{c}/{\sigma }_{c}+{\delta }_{e}-{\delta }_{p}\), the parameters \({\delta }_{e}\) and \({\delta }_{p}\) make it possible to determine the shape of the energy (see FIG. 8) and therefore the trapezoidal shape of the cohesive law (FIG. 9).
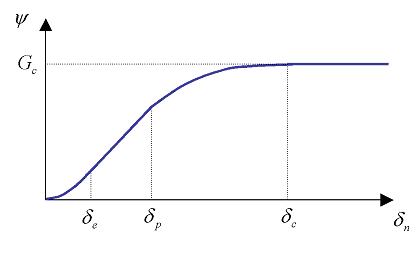
Figure8: Surface energy density as a function of the normal displacement jump, law CZM_TRA_MIX.
In practice, in Code_Aster, the user enters dimensionless parameters that correspond to a percentage of the critical jump. They are positive and strictly less than 1, baptized COEF_EXTR as extrinsic [4] _ to determine the slope at the origin (choice: infinite or not) and COEF_PLAS as plastic to determine the end of the plastic plateau of the law:
\({\delta }_{e}\) = COEF_EXTR. \({\delta }_{c}\)
\({\delta }_{p}\) = COEF_PLAS. \({\delta }_{c}\)
The critical jump is therefore deduced from the four material parameters provided by the user in the following way:
\({\delta }_{c}\mathrm{=}\frac{{\mathrm{2G}}_{c}}{{\sigma }_{c}(1\mathrm{-}\text{COEF\_EXTR}+\text{COEF\_PLAS})}\)
Note that to ensure the trapezoidal shape it is necessary to have the condition: COEF_EXTR less than COEF_PLAS. However, it is allowed for these two coefficients to be equal, which leads to a triangle shape. In addition, they must be strictly less than 1 in order to guarantee the uniqueness of the local solution.
If we choose a null COEF_EXTR, the first line of () is no longer relevant and if we also choose COEF_PLAS null, the second line is no longer useful. This scenario makes it possible to fall back on the energy of the fragile law CZM_OUV_MIX (see part 3.2.1). However, the irreversibility for contact is different. In fact, in ductile law, a residual jump \({\delta }_{\mathrm{res}}\) is retained when the lips are brought into contact (see next part).
3.3.2. Constraint vector#
The surface energy defined above cannot be derived in the following cases: \({\delta }_{n}=0\) (perfect adhesion before initiating if \({\delta }_{e}\mathrm{=}0\) or in the case of contact), and (\({\delta }_{n}=\kappa\) (vertical discharge if \({\delta }_{e}=0\)). The stress vector noted \(\overrightarrow{\sigma }\) is then defined as belonging to the subdifferential (generalization of the concept of derivative) of the surface energy density.
This set coincides with the derivative at the points where it is differentiable and with a set of possible directional derivatives otherwise. For more details, refer to the interface elements doc R7.02.13.
|
|
|
|
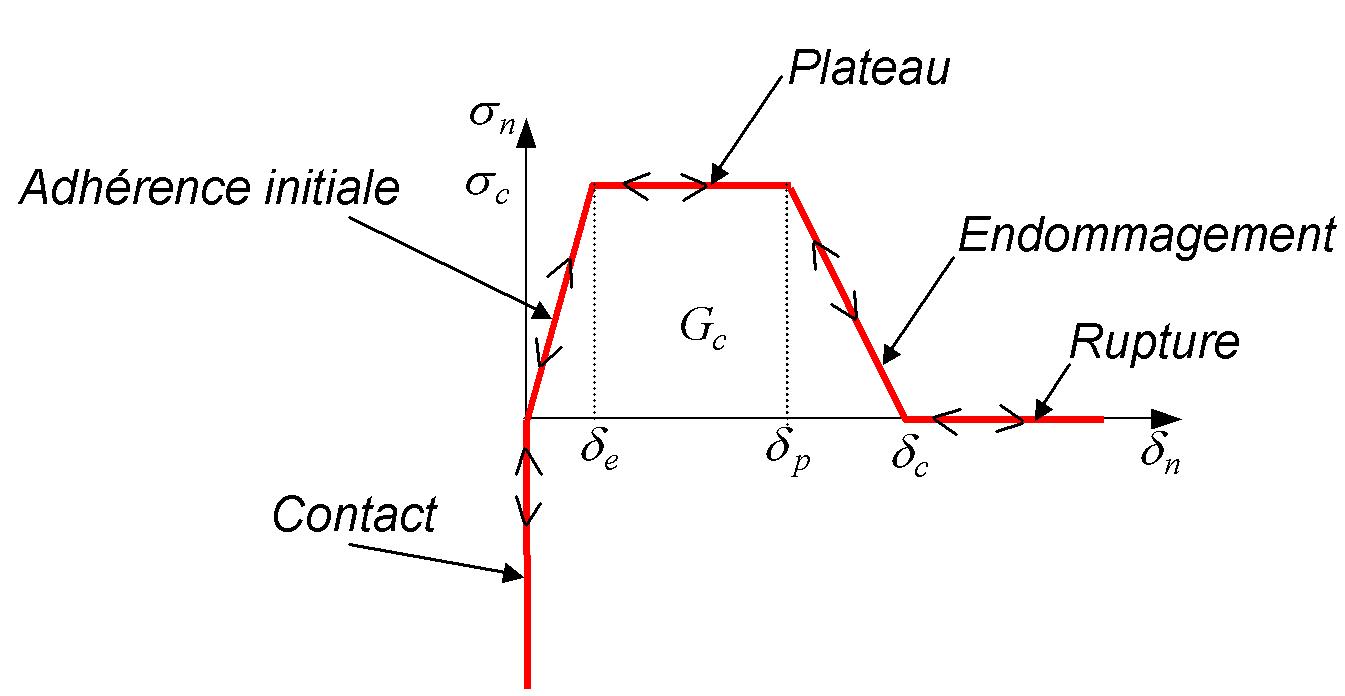
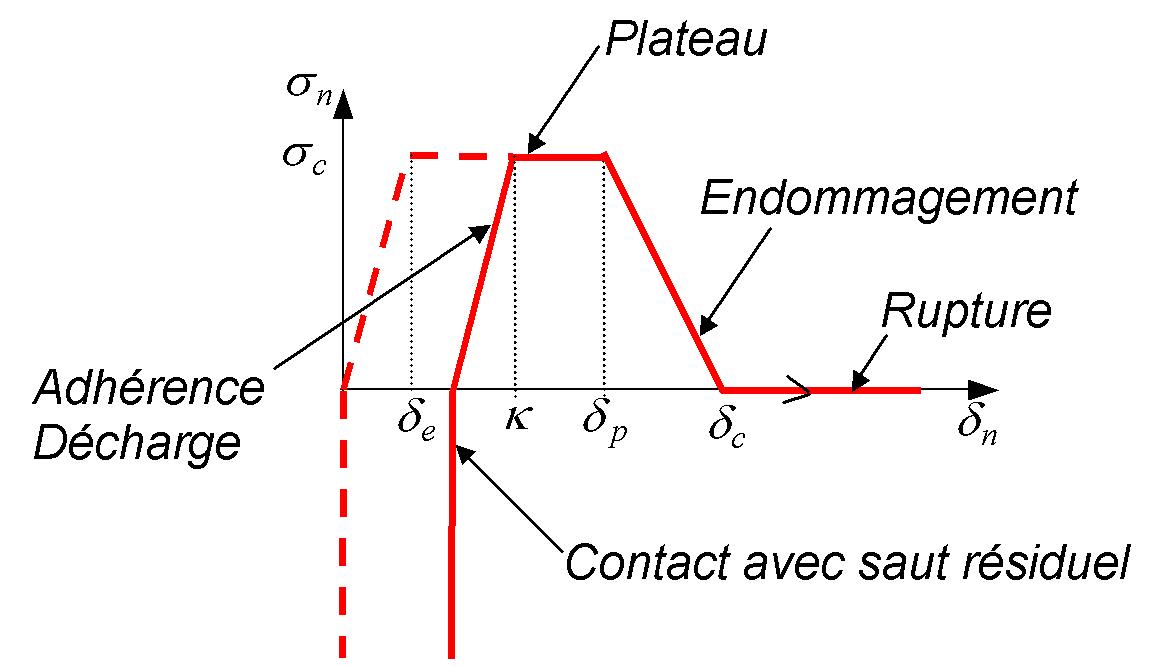
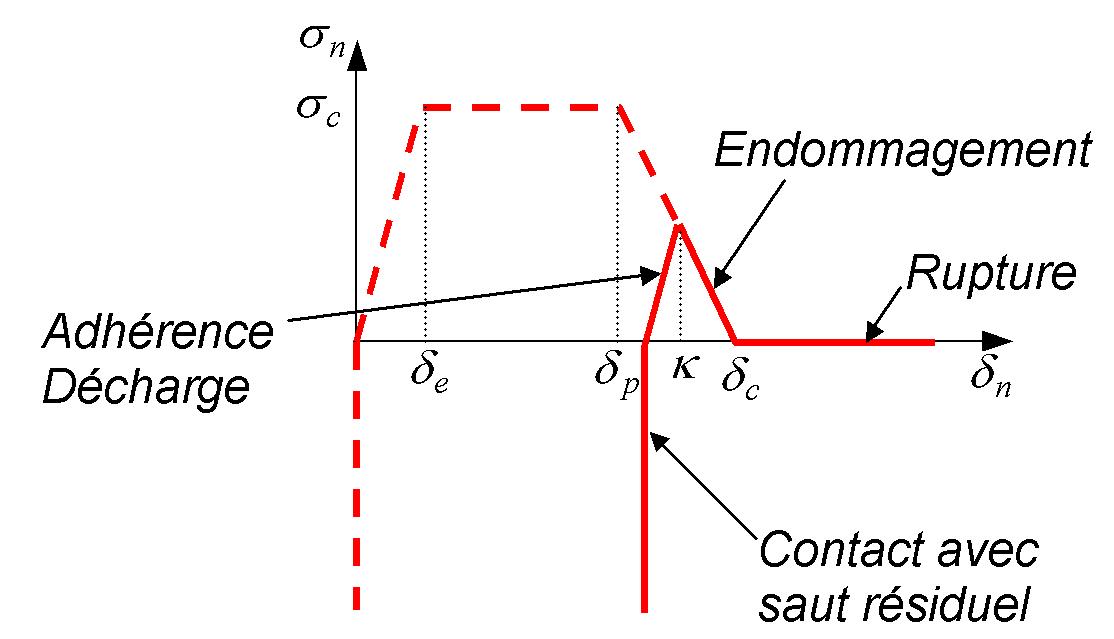
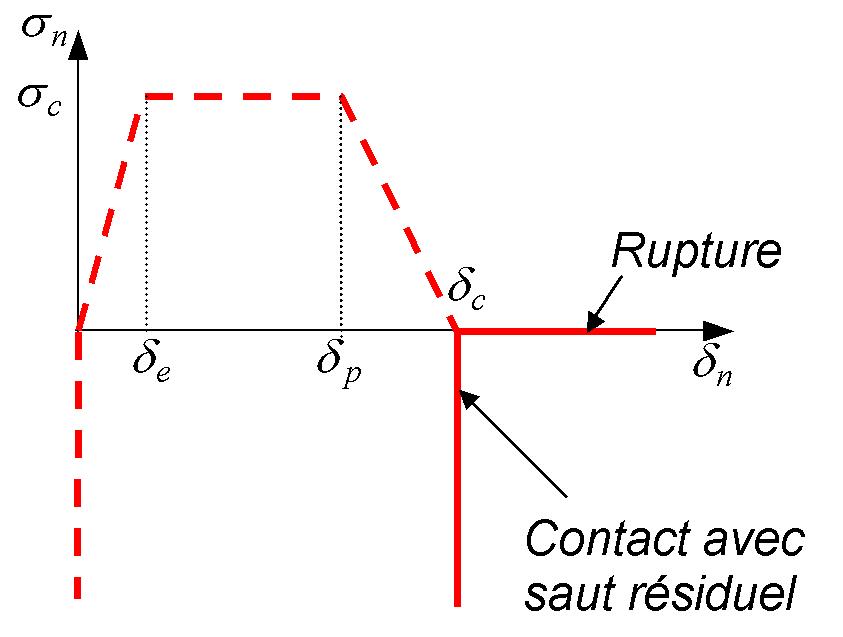
Figure9: Vector stress at different cracking states: healthy (9.1), damaged (9.2 and 9.3), and broken (9.4) .
In FIG. 9, the various stages of evolution of the law are represented in the case where \({\delta }_{e}\ne 0\). Otherwise, the initial grip and adhesion/discharge slopes are endless.
Definition of the evolution of the threshold
As we saw in the previous part, irreversibility is driven by a threshold noted \(\kappa\). Its initial value is fixed at \({\delta }_{e}\), in fact it is considered that there is no energy dissipation in the adhesion phase.
In the case where \({\delta }_{e}=0\), the evolution of the \(\kappa\) threshold, from one loading increment to another, is classically given by: \({\kappa }^{\text{+}}=\mathrm{max}({\kappa }^{\text{-}},{\delta }_{n})\)
In the case where \({\delta }_{e}\ne 0\) the evolution of the \(\kappa\) threshold, from one loading increment to another, is given by \({\kappa }^{\text{+}}=\mathrm{max}(\mathrm{max}({\kappa }^{\text{-}},{\delta }_{e}),{\delta }_{n})\).
In addition, the value of \(\kappa\) is limited to \({\delta }_{c}\).
These three points can be summarised in the following condensed text:
\({\kappa }^{\text{+}}=\mathrm{min}(\mathrm{max}(\mathrm{max}({\kappa }^{\text{-}},{\delta }_{e}),{\delta }_{n}),{\delta }_{c})\)
The threshold variable allows us to define the three states of the cohesive crack (illustrated in Figure 9):
Health: \(\kappa ={\delta }_{e}\)
Damaged: \({\delta }_{e}<\kappa <{\delta }_{c}\)
Broken: \(\kappa ={\delta }_{c}\)
Definition of residual contact jump
In the event of discharge, the choice is made to maintain an irreversible residual jump noted \({\delta }_{\mathrm{res}}\) to take account of the contact (see FIG. 9). This is motivated from a mechanical point of view. In fact, it is considered that the fasciae of the ductile rupture are quite hectic and that the crack lips do not stick together perfectly during a reclosing. The residual jump is defined as follows (see FIG. 10):
\({\delta }_{\mathrm{res}}=\kappa -{\delta }_{e}{\sigma }_{\kappa }/{\sigma }_{c}\)
with \({\sigma }_{\kappa }\) the current value of the critical constraint of the law, this quantity is given by:
\({\sigma }_{\kappa }=\mathrm{max}(0,\mathrm{min}({\sigma }_{c},{\sigma }_{c}(\frac{\kappa -{\delta }_{c}}{{\delta }_{p}-{\delta }_{c}})))\)
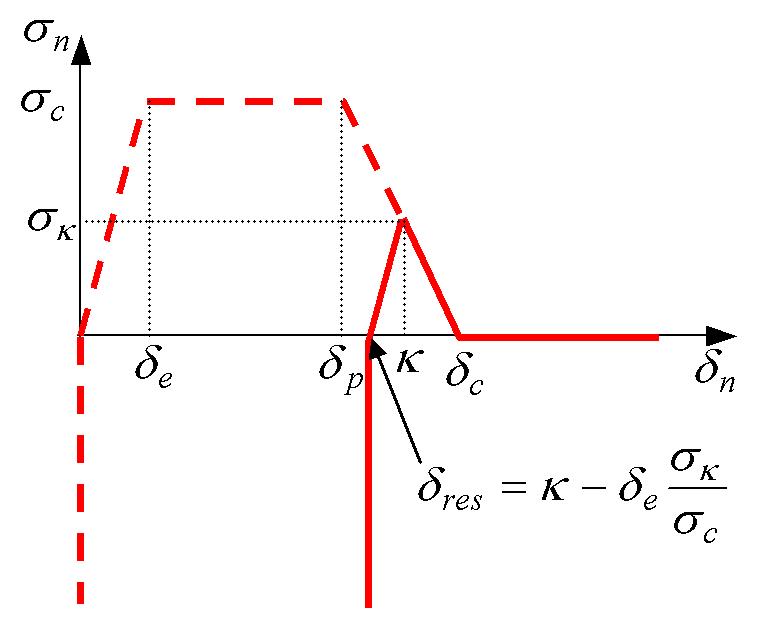
Figure 10: Cohesive law for a damaged state.
Remarks: In the « healthy » case, the contact is logically taken into account from a zero jump (see figure 9.1). In the « broken » case, the residual contact jump corresponds to the critical crack opening jump \({\delta }_{c}\) (see figure 9.4).
Definition of cohesive law:
Based on the quantities introduced previously, it is possible to adopt a description of the normal stress as a function of the normal opening in general, valid for the three states of cracking:
CZM_TRA_MIX : \(\begin{array}{}{\sigma }_{n}({\delta }_{n})\{\begin{array}{cc}\in \text{]}-\infty \mathrm{,0}\text{]}& \text{si}{\delta }_{n}={\delta }_{\mathrm{res}}\text{et}{\delta }_{e}\ne 0\text{contact}\\ \in \text{]}-\infty ,{\sigma }_{\kappa }\text{]}& \text{si}{\delta }_{n}={\delta }_{\mathrm{res}}\text{et}{\delta }_{e}=0\text{contact + adhésion parfaite}\\ =\frac{{\sigma }_{c}}{{\delta }_{e}}({\delta }_{n}-\kappa )+{\sigma }_{\kappa }& \text{si}{\delta }_{\mathrm{res}}<{\delta }_{n}\le \kappa \text{et}{\delta }_{e}\ne 0\text{adhésion extrinsèque}\\ =\mathrm{min}({\sigma }_{c},{\sigma }_{c}\frac{{\delta }_{n}-{\delta }_{c}}{{\delta }_{p}-{\delta }_{c}})& \text{si}\kappa <{\delta }_{n}\le {\delta }_{c}\text{dissipation}\\ =0& \text{si}{\delta }_{n}>{\delta }_{c}\text{rupture finale}\end{array}\end{array}\) |
\({\sigma }_{T}({\delta }_{T})=C{\delta }_{T}\text{où}T=t\text{ou}\tau \text{( comportement élastique)}\) (see 3.5 for the definition of \(C\))
In cases where energy is differentiable, the tangent modulus is easy to determine. Let us give the value of the latter for the phases of adhesion, dissipation and rupture:
\(\frac{\partial {\sigma }_{n}}{\partial {\delta }_{n}}\{\begin{array}{cc}=\frac{{\sigma }_{c}}{{\delta }_{e}}& \text{si}{\delta }_{\mathrm{res}}<{\delta }_{n}\le \kappa \text{et}{\delta }_{e}\ne 0\text{adhésion extrinsèque}\\ =\frac{{\sigma }_{c}}{{\delta }_{p}-{\delta }_{c}}& \text{si}{\delta }_{n}>{\delta }_{p}\text{et}\kappa <{\delta }_{n}\le {\delta }_{c}\text{dissipation adoucissant}\\ =0& \text{si}\kappa <{\delta }_{n}<{\delta }_{p}\text{dissipation plateau}\\ =0& \text{si}{\delta }_{n}>{\delta }_{c}\text{rupture finale}\end{array}\) \(\frac{\partial {\sigma }_{T}}{\partial {\delta }_{T}}=C\)
3.4. Cohesive law for fatigue CZM_FAT_MIX#
This law is intended to model crack propagation by fatigue in mode I. It is similar to those presented above. The main difference relates to the irreversibility of the cracking. The latter is based on the accumulation of openings during the loading cycles. This ingredient is essential for reporting fatigue with cohesive models. For theoretical information on this point, the reader can refer to Jaubert and Marigo (4).
3.4.1. Surface energy#
Surface energy \(\Psi\), defined on a \(\Gamma\) discontinuity, depends on the normal displacement jump between the lips of the crack: \({\delta }_{n}\) and on \(\kappa\) threshold internal variable that manages the irreversibility of the crack. The latter remembers the total number of openings during the loading cycles. Its law of evolution between two successive loading increments i and i+1 is written as:
\(\dot{\kappa }=\langle \dot{{\delta }_{n}}\rangle\)
where the operator \(\langle \mathrm{.}\rangle\) designates the positive part and the point the difference between the values in i and i+1. So \(\kappa\) only evolves when the normal jump increases and remains constant otherwise.
Surface energy is defined as follows:
with surface energy density:
\(\Pi ({\delta }_{n},\kappa )=\psi (\kappa )+{I}_{{ℝ}^{\text{+}}}({\delta }_{n})\)
where \({I}_{{ℝ}^{\text{+}}}\) indicator function translating the condition of non-interpenetration of the lips of the crack:
\({I}_{{ℝ}^{\text{+}}}({\delta }_{n})=\{\begin{array}{}+\infty \text{si}{\delta }_{n}<0\\ 0\text{si}{\delta }_{n}\ge 0\end{array}\)
and \(\psi\) cohesive energy density defined as follows:
: label: EQ-None
: label: eq-27
textrm {CZM_FAT_MIX:} begin {array} {}psi (kappa) ={begin {array} {cc}frac {- {sigma} _ {c} ^ {2}} {4 {G} _ {c}}} {c}} {kappa}}} {kappa}}} {kappa} ^ {2}} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2} + {sigma} _ {2}sigma} _ {c}\ {G} _ {c} _ {c} &text {c} &text {si}\ text {si}\ text {c}end {array}\ psi ({delta} _ {T}) =frac {1} {T}) =frac {1} {T} {T} {T}) =frac {1} {T} {T}) =frac {1} {T} {T}) =frac {1} {T} {2} T=ttext {or}Tauend {array}
Note:
We introduce a rigidity \(C\) in sliding mode for numerical questions. This break mode does not dissipate energy and is not intended to be activated.
:math:`C`*depends on a numerical parameter chosen by the user (see part:ref:`3.5 <Ref207599345>`*) *
3.4.2. Constraint vector#
The surface energy defined above is not differentiable with respect to the jump in the following cases: \({\delta }_{n}=0\) (priming) and \(\dot{{\delta }_{n}}=0\) (the jump does not evolve). The stress vector noted \(\overrightarrow{\sigma }\) is defined as belonging to the subdifferential (generalization of the concept of derivative) of the surface energy density.
This set coincides with the derivative at the points where it is differentiable:
\({\sigma }_{n}({\delta }_{n})=\frac{\partial \psi }{\partial \kappa }\frac{\partial \kappa }{\partial {\delta }_{n}}\)
with \(\begin{array}{}\frac{\partial \psi }{\partial \kappa }\end{array}=\{\begin{array}{cc}{\sigma }_{c}\text{}(1-\frac{\kappa }{{\delta }_{c}})& \text{si}\kappa <{\delta }_{c}\\ 0& \text{si}\kappa \ge {\delta }_{c}\end{array}\), \(\begin{array}{}\frac{\partial \kappa }{\partial {\delta }_{n}}\end{array}=\{\begin{array}{cc}1& \text{si}\dot{{\delta }_{n}}>0\text{et}{\delta }_{n}\ne 0\\ 0& \text{si}\dot{{\delta }_{n}}<0\text{et}{\delta }_{n}\ne 0\end{array}\), and \({\delta }_{c}=2{G}_{c}/{\sigma }_{c}\)
and to a set of possible directional derivatives in the opposite case. For more details, refer to the interface elements doc R7.02.13. For the law CZM_FAT_MIXles modes are decoupled, we explain the sub-differentials (sets of scalars) for each of them:
Fashion \(I\) :
Adhesion before priming (\(\kappa =0\) and \({\delta }_{n}=0\)):
\(\partial \Pi ({\delta }_{n})=\{{x}_{n}\in ℝ;{x}_{n}\le {\sigma }_{c}\}\)
Charge/discharge back to zero (\(\dot{{\delta }_{n}}<0\)) and contact condition:
\(\partial \Pi ({\delta }_{n})=\{{x}_{n};{x}_{n}\le 0\text{et}{\delta }_{n}\ge 0\text{et}{x}_{n}{\delta }_{n}=0\}\)
Vertical charge/discharge (\(\dot{{\delta }_{n}}=0\)):
\(\partial \Pi ({\delta }_{n})=\{\lambda {\delta }_{n};0\le \lambda \le \frac{\psi \text{'}(\kappa )}{\kappa }\}\)
Damage and breakage (\(\dot{{\delta }_{n}}>0\)):
\(\partial \Pi ({\delta }_{n})=\{\psi \text{'}(\kappa )\}\)
Fashion \(\mathit{II}\) or \(\mathit{III}\) :
Linear behavior:
\(\partial \Pi ({\delta }_{T})=\{\psi \text{'}({\delta }_{T})\}\text{, T =}t\text{ou}\tau\)
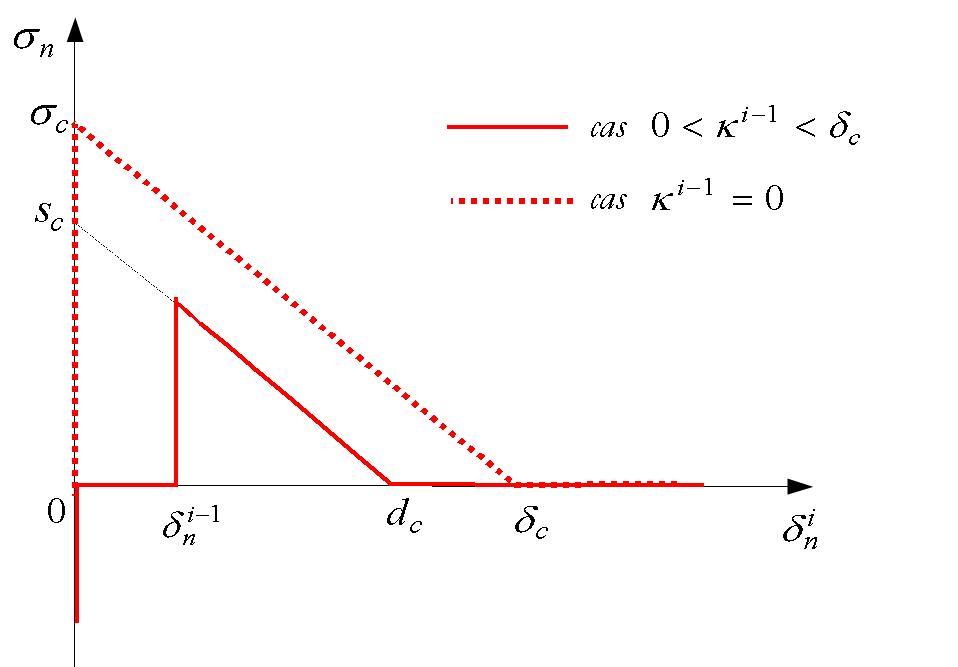
Figure11: Form of cohesive law CZM_FAT_MIX
We can present the cohesive law CZM_FAT_MIXen adopting a more usual form of writing. The normal stress \({\sigma }_{n}\) is expressed as a function of the current jump \({\delta }_{n}^{\text{i}}\) for various values of the threshold at the previous instant \({\kappa }^{\text{i-1}}\) (see FIG. 11):
Cas \({\kappa }^{\text{i-1}}=0\): priming configuration (dotted line in FIG. 11)
\(\begin{array}{}{\sigma }_{n}({\delta }_{n}^{\text{i}})\end{array}=\{\begin{array}{cc}{\sigma }_{c}\text{}(1-\frac{{\delta }_{n}^{\text{i}}}{{\delta }_{c}})& \text{si}0<{\delta }_{n}^{\text{i}}\le {\delta }_{c}\\ 0& \text{si}{\delta }_{n}^{\text{i}}>{\delta }_{c}\end{array}\) and \({\sigma }_{n}(0)\le {\sigma }_{c}\) priming condition
Cas \(0<{\kappa }^{\text{i-1}}<{\delta }_{c}\): current configuration (solid line in Figure 11)
\(\begin{array}{}{\sigma }_{n}({\delta }_{n}^{\text{i}})\end{array}=\{\begin{array}{cc}0& \text{si}0<{\delta }_{n}^{\text{i}}<{\delta }_{n}^{\text{i-1}}\\ {\sigma }_{c}\text{}(1-\frac{{\kappa }^{\text{i-1}}+{\delta }_{n}^{\text{i}}-{\delta }_{n}^{\text{i-1}}}{\text{}{\delta }_{c}})& \text{si}{\delta }_{n}^{\text{i-1}}<{\delta }_{n}^{\text{i}}\le {d}_{c}\\ 0& \text{si}{\delta }_{n}^{\text{i}}>{d}_{c}\end{array}\) with \(\{\begin{array}{c}{d}_{c}={\delta }_{c}{s}_{c}/{\sigma }_{c}\\ {s}_{c}={\sigma }_{c}\text{}(1-\frac{{\kappa }^{\text{i-1}}-{\delta }_{n}^{\text{i-1}}}{\text{}{\delta }_{c}})\end{array}\),
and contact condition \({\sigma }_{n}(0)\le 0\),
and vertical charge/discharge condition \(0\le {\sigma }_{n}({\delta }_{n}^{\text{i}})<{\sigma }_{c}\text{}(1-\frac{{\kappa }^{\text{i-1}}}{{\delta }_{c}})\)
Case \({\kappa }^{\text{i-1}}\ge {\delta }_{c}\) : configuration break
\({\sigma }_{n}({\delta }_{n}^{\text{i}})=0\text{si}{\delta }_{n}^{\text{i}}>0\) and contact condition \({\sigma }_{n}(0)\le 0\)
By way of illustration, a cyclic evolution of a constant amplitude of the normal displacement jump on a gauss point leads to the evolution of the stress represented in FIG. 12. It also shows the case where the load is monotonic. The evolution of the stress is then identical to that during the first increase in the cyclic load. Which brings us to the next remark:
Note:
The law CZM_FAT_MIXest equivalent to the law CZM_OUV_MIXtant that loading is monotonous. However, this condition cannot be guaranteed at each gauss point, since it can be subject to local discharges of the structure even if the overall load increases. It is therefore not recommended to use the law of fatigue to model cracking under monotonous load.The risk is not to obtain the same result as with the law CZM_OUV_MIX.
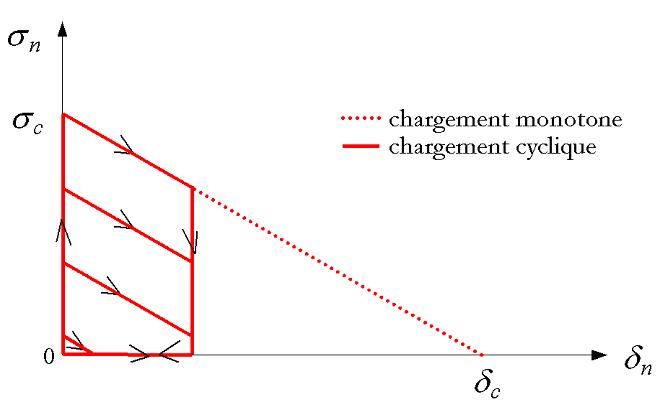
Figure12: Evolution of stress during monotonic and cyclic loading with law CZM_FAT_MIX
3.5. Numeric parameters PENA_LAGR and RIGI_GLIS#
The augmented Lagrangian formulation of the model introduces a numerical penalty parameter, noted PENA_LAGR in Code_Aster. This value, entered by the user under the keyword RUPT_FRAG, is linked to the scalar that multiplies the quadratic term of the Lagrangian (noted \(r\) in the R3.06.13 documentation) by the following relationship:
\(r\mathrm{=}\text{PENA\_LAGR}\mathrm{.}{\sigma }_{c}^{2}\mathrm{/}2{G}_{c}\)
Note:
It is required PENA_LAGR to be strictly greater than 1 for the problem to be well posed (uniqueness of the solution). For more details on this point, refer to doc R3.06.13 or to ( 6 ) .
For laws CZM_OUV_MIX, CZM_FAT_MIX and CZM_TRA_MIXun other numerical parameter is required (in addition to the previous one), it determines the stiffness of the sliding behavior (parameter \(C\) introduced in part 3.2.1). We note it RIGI_GLIS, it is linked to \(C\) by:
\(C=\text{RIGI\_GLIS}\mathrm{.}{\sigma }_{c}^{2}/2{G}_{c}\)
It should be noted that the purpose of these two laws is to take into account the dissipation of energy by cracking in open mode only. The rigidity of the sliding only intervenes to numerically treat the case where it is desired to impose symmetry conditions on the interface elements. The objective is to maintain sliding stiffness when the element is broken when opened.
3.6. Internal variables#
Laws CZM_xxx_MIX each have nine internal variables. From the point of view of the law of behavior, only the former is*stricto sensu* an internal variable. The others provide information on the state of the interface element at a given moment.
\(\mathrm{V1}=\kappa\): jumping threshold, allows you to take into account the irreversibility of the cracking, see its definition in the previous parts (specific to each law).
\(\mathrm{V2}\): law regime indicator
For laoi CZM_TRA_MIX \(\mathrm{V2}=-1\): contact, \(\mathrm{V2}=0\): contact,: initial or current adhesion, \(\mathrm{V2}=1\): dissipation, \(\mathrm{V2}=2\): final break, \(\mathrm{V2}=3\): plateau (see figure 13).
For the other laws CZM_xxx_MIX: \(\mathrm{V2}=-1\): contact, \(\mathrm{V2}=0\): contact,: initial or current adhesion, \(\mathrm{V2}=1\): dissipation, \(\mathrm{V2}=2\): final rupture, \(\mathrm{V2}=3\): return to zero at zero stress (see figure 13).
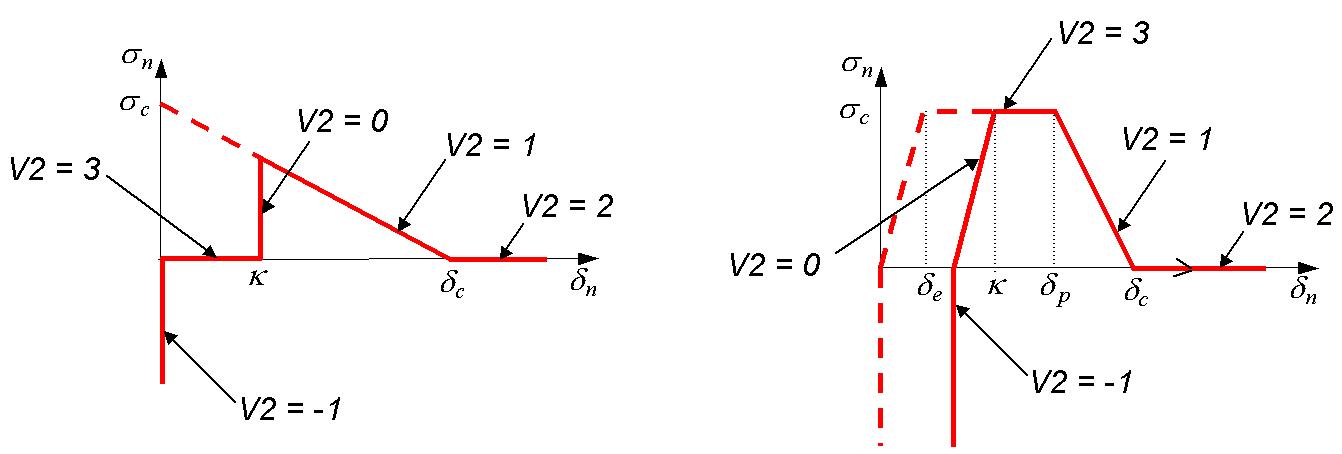
Figure13: Representation of the values of the V2 indicator for laws CZM_OUV_MIX on the left and CZM_TRA_MIX on the right
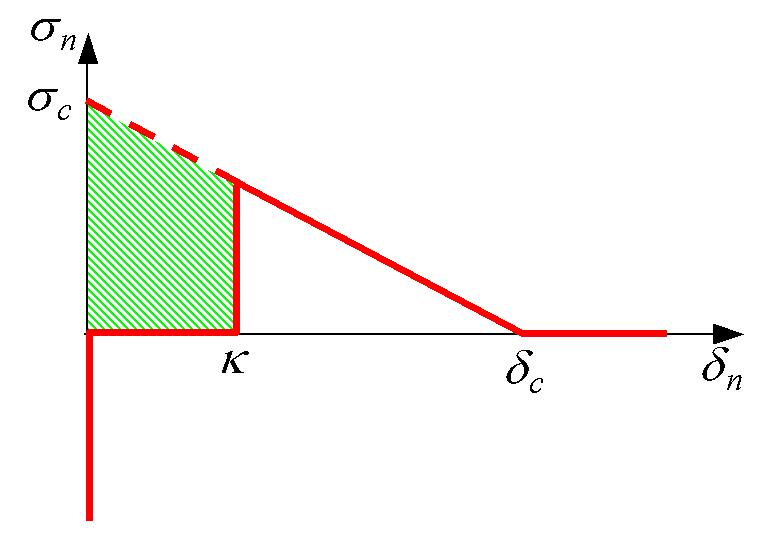
\(\mathrm{V3}\): damage indicator \(\mathrm{V3}=0\) if material is healthy, \(\mathrm{V3}=1\) if material is healthy, if material is damaged, \(\mathrm{V3}=2\) if material is broken (see examples figures 9.1, 9.2 and 9.4 for CZM_TRA_MIX and figure 7 for CZM_OUV_MIX).
\(\mathrm{V4}\): percentage of energy dissipated.
\(\mathrm{V4}=\frac{\kappa {\sigma }_{c}}{{G}_{c}}(1-\frac{\kappa {\sigma }_{c}}{4{G}_{c}})\) for CZM_OUV_MIX and CZM_TAC_MIX
\(\mathrm{V4}=\frac{{\delta }_{\mathrm{res}}({\sigma }_{c}+{\sigma }_{\kappa })+({\delta }_{p}-{\delta }_{e})({\sigma }_{c}-{\sigma }_{\kappa })}{2{G}_{c}}\) for CZM_TRA_MIX
\(\mathrm{V5}=\mathrm{V4}\times {G}_{c}\): value of dissipated energy (see figure 14).
\(\mathrm{V6}\): value of current residual energy: zero for these laws (valid for CZM_xxx_REG).
\(\mathrm{V7}={\delta }_{n}\): normal jump, \(\mathrm{V8}={\delta }_{t}\): tangential hop, \(\mathrm{V9}={\delta }_{\tau }\) tangential hop (null in 2D).
|
|
Figure14: Representation of the energy dissipated V5 (shaded part) for laws CZM_OUV_MIXet CZM_TRA_MIX
Note:
For the law CZM_FAT_MIXl the energy dissipated is equal to the sum of the areas of the trapezius during the evolution of the stress shown in FIG. 12. Once the material point is broken, we notice that this energy is equal to the area of the triangle described during a monotonic evolution.
3.7. Cohesive law for a steel-concrete bond CZM_LAB_MIX#
3.7.1. Surface energy#
This model was designed to model the behavior of a steel-concrete bond in a reinforced concrete structure. We can refer to (9) for the construction and validation of this model.
The surface energy \(\Psi\), defined on an interface \(\Gamma\), depends on the displacement jump through the interface \(\delta\) and on the internal threshold variable \(\kappa\) which manages the irreversibility of the sliding. The latter remembers the greatest jump norm reached during the slide. Its law of evolution between two successive loading increments - and + is written as:
\({\kappa }^{\text{+}}\mathrm{=}\text{max}({\kappa }^{\text{-}},\mathrm{\parallel }\delta \mathrm{\parallel })\)
Surface energy is defined as follows:
with surface energy density:
\(\Pi (\delta ,\kappa )\mathrm{=}\psi (\text{max}(\mathrm{\parallel }\delta \mathrm{\parallel },\kappa ))+{I}_{{\mathrm{ℝ}}^{\text{+}}}(\delta )\)
where \({I}_{{ℝ}^{\text{+}}}\) is an indicator function that imposes the sliding kinematics of the interface. The various possible kinematics (at the user’s choice) are mentioned in the table below:
Unilateral contact |
\({I}_{{ℝ}^{\text{+}}}(\delta )=\{\begin{array}{c}+\infty \text{si}{\delta }_{n}<0\\ 0\text{si}{\delta }_{n}\ge 0\end{array}\) |
|
Sliding in the tangential plane |
\({I}_{{ℝ}^{\text{+}}}(\delta )=\{\begin{array}{c}+\infty \text{si}{\delta }_{n}\ne 0\\ 0\text{si}{\delta }_{n}=0\end{array}\) |
|
Unidirectional sliding according to the vector \(t\) |
|
The cohesive energy density \(\psi\) is such that:
This quantity is interpreted as the cohesive force at the interface as a function of the displacement jump, and is represented in FIG. 15. The parameters \({\sigma }_{0}\) and \({\delta }_{0}\) allow the force and displacement to be dimensioned, while \(\alpha\) and \(\beta\) configure the shape of the curve. In practice, you have to have \(0<\alpha <1\) and \(\beta >0\).
We can calculate the point where the cohesive force is maximum, which is defined by:
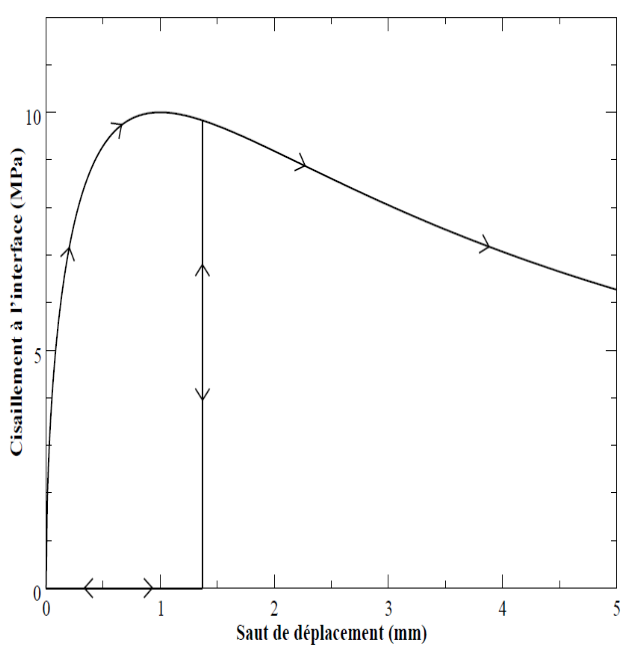
Figure15 : Cohesive force according to the norm of the displacement jump, law CZM_LAB_MIX.
\(\{\begin{array}{c}{\sigma }_{c}=\frac{{\alpha }^{\alpha }{\beta }^{\beta }}{{(\alpha +\beta )}^{\alpha +\beta }}{\sigma }_{0}\\ {\delta }_{c}=\frac{\alpha }{\beta }{\delta }_{0}\end{array}\)
3.7.2. Constraint vector#
The surface energy defined above is not differentiable when \(\mathrm{\parallel }\delta \mathrm{\parallel }\mathrm{=}\kappa\) (vertical discharge of the Talon-Curnier type) as well as at the points of discontinuity of the indicator \({I}_{{\mathrm{ℝ}}^{\text{+}}}\). The stress vector noted \(\sigma\) is then defined as belonging to the subdifferential (generalization of the concept of derivative) of the surface energy density.
This set coincides with the derivative at the points where it is differentiable and with a set of possible directional derivatives otherwise. For more details, refer to the interface elements doc R7.02.13. Let us specify here the values taken by this set when the law imposes a unidirectional sliding in the direction of the vector \(t\):
Damage (\(\mathrm{\parallel }\delta \mathrm{\parallel }\mathrm{=}\kappa\) and \(\dot{\mathrm{\parallel }\delta \mathrm{\parallel }}>0\)):
\(\mathrm{\partial }\Pi (\delta )\mathrm{=}\mathrm{\{}t\mathrm{.}\sigma \mathrm{.}n\mathrm{=}\mathrm{-}\mathit{sgn}(t\mathrm{.}\delta )\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\delta }(\mathrm{\parallel }\delta \mathrm{\parallel })\mathrm{\}}\)
Vertical unload/recharge (\(\mathrm{\parallel }\delta \mathrm{\parallel }\mathrm{=}\kappa\) and \(\dot{\mathrm{\parallel }\delta \mathrm{\parallel }}\mathrm{=}0\)):
\(\mathrm{\partial }\Pi (\delta )\mathrm{=}\mathrm{\{}t\mathrm{.}\sigma \mathrm{.}n\mathrm{=}\mathrm{-}\mathit{sgn}(t\mathrm{.}\delta )\lambda \text{avec}0<\lambda <\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\delta }(\kappa )\mathrm{\}}\)
Zero stress discharge/recharge (\(\mathrm{\parallel }\delta \mathrm{\parallel }<\kappa\)):
\(\mathrm{\partial }\Pi (\delta )\mathrm{=}\mathrm{\{}t\mathrm{.}\sigma \mathrm{.}n\mathrm{=}0\mathrm{\}}\)