4. Mechanical touch/friction problem

Taking contact and friction into account in a mechanical problem has two consequences:

• The modification of the equilibrium equation to take into account touch-friction reactions at interfaces;

• The application of additional laws governing contact and friction (see § 2) to calculate these reactions but also to impose conditions on kinematics.

For frictionless contact, the Signorin conditions boil down to a classical stress optimization problem (Kuhn & Tucker). On the other hand, for Coulomb friction, one cannot write an equivalent optimization problem without making additional hypothesis (s).

In Code_Aster, discrete methods for solving the touch/friction problem are based on an decouple approach between balance and the law of touch/friction. After solving the mechanical problem without touch-friction, we correct the solution (kinematics and reactions) by applying the Signorini-Coulomb law. This strategy makes it possible to make no other hypothesis about the nature of the mechanical problem, whether it be kinematics or behavioral relationships. However, it is essential that the stiffness matrix of the non-contact problem be symmetric.

Notes:

• The expression « perform a contact calculation » means that non-penetration relationships are written, but does not mean that there is effective contact for the load in question. However, it is the resolution of the contact and friction problem that is the most expensive.

• Since contact acts as a correction on the results obtained from a classical mechanical calculation, it is essential that the contactless problem be mechanically well posed and numerically solvable. In particular, any rigid body movements must be assumed to be eliminated without resolving the contact problem.

4.1. Mechanical problem without touch/friction

Solving a non-linear problem in the STAT_NON_LINE (or DYNA_NON_LINE) operator is described in detail in document [R5.03.01]. At each \(i\) time step, we try to check the overall balance of the structure:

(4.1)\[\begin{split} \ mathrm {\ {}\ begin {array} {c}\ left\ {{L} _ {{L} _ {i} ^ {\ text {int}} ({u} _ {i})\ right\}\ right\}} + {\ left [B\ right]} + {\ left [B\ right]} + {\ left [B\ right]} + {\ left [B\ right]}} ^ {T}\ mathrm {.} \ left\ {{\ lambda} _ {i}\ right\}\ right\}\ mathrm {=}\ left\ {{L} _ {i} ^ {\ text {mecha}}} ({u} _ {i})\ right\ {i})\ right\ {i})\ right\ {i})\ right\ {i})\ right\}\\ left [B\ right]\ mathrm {.} \ left\ {{u} _ {i}\ right\}\ right\}\ mathrm {=}\ left\ {{u} _ {i} ^ {d}\ right\}\ right\}\ right\}\ end {array}\end{split}\]

In order to avoid overloading the equations, we make the assumption that the boundary conditions are eliminated and where we therefore do not have a \(\left[B\right]\) matrix, we therefore try to solve:

(4.2)\[ \ left\ {{L} _ {i} ^ {\ text {int}}} ({u} _ {i})\ right\} =\ left\ {{L} _ {i} ^ {\ text {mecha} ^ {\ text {mecha}}} ({u} _ {i})\ right\} ^ {\ text {mecha}} ^ {\ text {mecha}}} ({u} _ {i})\ right\}\]

This non-linear problem is solved by an iterative Newton-Raphson method which has the following characteristics:

An*a priori division of the load into « time steps » (noted by the index \(i\));

• A linearization of the balance problem by Newton’s method (the iterations being noted by the index \(n\)).

The unknowns are calculated incrementally. Starting with \(\left\{{u}_{i\mathrm{-}1}\right\}\), a solution satisfying the balance in \({t}_{i-1}\), we determine \(\left\{\Delta {u}_{i}\right\}\) which makes it possible to obtain the solution in \({t}_{i}\):

(4.3)\[ \ left\ {{u} _ {i}\ right\}\ right\}\ mathrm {=}\ left\ {{u} _ {i\ mathrm {-} 1}\ right\} +\ left\ {\ right\} +\ left\ {\ right\} +\ left\ {\ Delta {u} _ {i}\ right\}\]

Increment \(\left\{\Delta {u}_{i}\right\}\) is first estimated by linearizing the problem with respect to time around \((\left\{{u}_{i\mathrm{-}1}\right\},{t}_{i\mathrm{-}1})\) (prediction or Euler phase). Then we use a Newton method or one of its variants to solve equation () iteratively: we calculate a sequence \(\left\{\delta {u}_{i}^{n}\right\}\) where the exponent \(n\) is the iteration number. To simplify, no distinction will be made between the prediction phase and the Newton correction phase. Finally, we write:

(4.4)\[ \ left\ {{u} _ {i} ^ {n}\ right\}\ right\}\ right\}\ mathrm {=}\ left\ {{u} _ {i\ mathrm {-} 1}\ right\}} +\ left\ {left\ {\ delta {u}} +\ left\ {\ delta {u}} +\ left\ {\ delta {u}} +\ left\ {\ delta {u} {u}\ left\ {\ delta {u} {u} +\ left\ {\ delta {u} {u}\ left\ {\ delta {u} {u}\ left\ {\ delta {u} {u}\ right\}\]

Let’s move on to time \({t}_{i}\) and Newton’s iteration \(n\). The following notations were used:

• \(\left\{{u}_{i}^{n}\right\}\): moves at time \({t}_{i}\) and at Newton iteration \(n\);

• \(\left\{{u}_{i\mathrm{-}1}\right\}\): move to instant \({t}_{i-1}\). This solution respects the condition of balance of the structure;

• \(\left\{\delta {u}^{n}\right\}\): increment of the movements for Newton iteration \(n\);

• \(\left\{\Delta {u}_{i}^{n\mathrm{-}1}\right\}\): increment of the accumulated displacements since the start of the time step, before the Newton iteration \(n\);

After linearization of (), for the Newton iteration \(n\), we introduce [bib5] _ the mechanical tangent matrix \(\left[{K}^{\text{m},n\mathrm{-}1}\right]\) we must then find \(\left\{\delta {u}^{n}\right\}\) such that:

\[\]

: label: eq-50

left [{K} ^ {text {m}, nmathrm {-} 1}right]text {.} left{delta {u} ^ {n}right}right}mathrm {=}left{{L} _ {i} ^ {text {mecha}, nmathrm {-} 1}rightright}right}right}right}right}right}}right}right}}right}

4.2. Modification of the equilibrium equation with contact/friction

To ensure the balance of the structure, contact/friction forces must be introduced. As generally as possible, it is written that the mechanical external load is modified by the contact/friction forces:

(4.5)\[ \ left\ {{L} _ {i} ^ {\ text {mecha}} ({u} _ {i})\ right\}\ mathrm {=}\ left\ {{L} _ {i} _ {i} ^ {i} ^ {i} ^ {i} ^ {ext}}} ({u} _ {i}}} ({u} _ {i}}) ({u} _ {i}}) ({u} _ {i}})\ right\}\ mathrm {-}\ left\ {{L} _ {i} _ {i} ^ {text} ^ {ext}}} ({u} _ {i}}} ({u} _ {i}})\ right\}\ mathrm {-}\ left\ {{L} _ {i} c}} ({u} _ {i})\ right\}\ right\}\ right\}\ right\}\ left\ {{L} _ {i} ^ {\ text {f}}} ({u} _ {i})\ right\}\]

Where:

• \(\left\{{L}_{i}^{\text{ext}}({u}_{i})\right\}\) is the vector of external forces (Neumann conditions);

• \(\left\{{L}_{i}^{\text{c}}({u}_{i})\right\}\) is the vector of contact forces;

• \(\left\{{L}_{i}^{\text{f}}({u}_{i})\right\}\) is the vector of frictional forces;

In principle, all these quantities are non-linear because they depend on the displacement vector \(\left\{{u}_{i}\right\}\) (we speak of « follower » loads). By injecting () into (), we therefore seek to solve:

\[\]

: label: eq-52

left{{L} _ {i} ^ {text {int}}} ({u} _ {int}}} ({u} _ {i})rightmathrm {=}left{{L} _ {i} _ {i} ^ {i} ^ {i} ^ {text {ext}}} ^ {text {ext}}}} ({u} _ {ext}}} ^ {u} _ {ext}}} ({u} _ {i}}} ({u} _ {i}}) ({u} _ {i}}) ({u} _ {i}}) ({u} _ {i}})right}mathrm {-}left{{L} _ {i} _ {i} ^ {i} ^}} ({u} _ {i})right}right}mathrm {-}left{{L} _ {i} ^ {text {f}}} ({u} _ {i})right}

At each Newton iteration \(n\), we linearize the equation () with respect to \(\left\{{u}_{i}^{n}\right\}\). This process introduces the tangent matrix \(\left[{K}^{\text{m},n\mathrm{-}1}\right]\) which will contain the contributions resulting from the linearization of internal and external forces and the matrix \(\left[{K}^{\text{cf},n\mathrm{-}1}\right]\) which will contain the contributions resulting from the linearization of the contact/friction forces, we must then find \(\left\{\delta {u}^{n}\right\}\) such that:

(4.6)\[ (\ left [{K} ^ {\ text {m}, n\ mathrm {-} 1}\ right] +\ left [{K} ^ {\ text {cf}, n\ mathrm {-} 1} 1}\ right])\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\}\ right\}\ mathrm {=}\ left\ {{L} _ {i} ^ {\ text {ext}, n\ mathrm {-} 1}\ right\ right\}\ right\}\ right\}\ mathrm {-}}\ right\ mathrm {-} 1}\ right\}\ mathrm {-}\ left\ {{L} _ {{L} _ {i} _ {i} ^ {\ text {c}, n\ mathrm {-}\ mathrm {-}\ left\ {{L}\ left\ {{L} _ {{L} _ {L} _ {i}} _ {i} ^ {i} ^ {\ text {f}, n\ mathrm {-} 1}\ right\}\]

4.3. Contact/friction laws

The laws of Signorin and Coulomb involve inequalities and equalities. The discrete formulation available in Code_Aster consists in changing relationships of inequality into relationships of equality. To do this, there are two possible methods:

1. Dualize the laws of touch/friction;

2. Regularize the laws of touch/friction.

4.3.1. Cinematics

4.3.1.1. Contact/friction matrices

In paragraph § 3.5.1, we saw how to write kinematic contact conditions by introducing the \(\left[{A}^{\text{c}}\right]\) contact matrix. In the same way, but considering the kinematic friction conditions (on the tangential plane), we will evaluate the sliding \(\left[{A}^{\text{g}}\right]\) and adhesion \(\left[{A}^{\text{a}}\right]\) matrices. These semi-full and rectangular matrices are calculated by evaluating the kinematic relationships between the slave node and the paired master mesh. The construction of kinematic relationships is done during the geometric matching procedure, which occurs at the beginning of each time step and at each geometric update. For reasons of performance, only the subpart of these matrices corresponding to the activation of the various thresholds (contact or sliding) is used and constructed, within the contact/friction resolution algorithms.

These matrices depend on the geometric update.

At the global level, matrices do not depend on the contactless solution of the mechanical problem.

4.3.1.2. Unilateral contact conditions

The non-penetration relationship consists in saying that relative displacement in a given direction cannot exceed the initial set \(\left\{{d}_{\text{ini}}^{\text{c}}\right\}\), measured on the mesh, in this direction. The unilateral contact condition is written (see § 3.5.1):

(4.7)\[ \ left [{A} ^ {\ text {c}}}\ right]\ text {.} \ left\ {{u} _ {i}\ right\}\ right\}\ mathrm {\ le}\ left\ {{d} _ {\ text {ini}}} ^ {\ text {c}}\ right\}\]

This equation reflects the fact that any movement of the structure must take place in compliance with the non-penetration condition, or that the displacement of the nodes of the contact surface is less than the initial set \(\left\{{d}_{\text{ini}}^{\text{c}}\right\}\). After solving the mechanical problem by Newton’s method, the non-penetration condition becomes:

(4.8)\[ \ left [{A} ^ {\ text {c}}}\ right]\ mathrm {.} (\ left\ {{u} _ {i\ mathrm {-} 1}\ right\} 1}\ right\} +\ left\ {\ Delta {u} _ {i} ^ {n\ mathrm {-} 1}\ right\} 1}\ right\} +\ left\ right\}\ left\ {{d}}} +\ left\ {{d}}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} +\ left\ {\ right\}} ^ {\ text {c}}\ right\}\]

This condition can be written iteratively:

(4.9)\[ \ left [{A} ^ {\ text {c}}}\ right]\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\}\ right\}\ mathrm {\ le}\ left\ {{d} ^ {\ text {c}, n\ mathrm {-} 1}\ right\}\]

With \(\left\{{d}^{\text{c},n\mathrm{-}1}\right\}\) the game evaluated before the current Newton iteration \(n\):

(4.10)\[ \ left\ {{d} ^ {\ text {c}}, n\ mathrm {-} 1}\ right\}\ right\ mathrm {=}\ left\ {{d} _ {\ text {ini}}}} ^ {\ text {ini}}}} ^ {\ text {ini}}}} ^ {\ text {ini}}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} ^ {\ text {ini}}} (\ left\ {{u} _ {i\ mathrm {-} 1}\ right\} +\ left\ {\ Delta {u} _ {i} ^ {n\ mathrm {-} 1}\ right\})\]

4.3.1.3. Adherence conditions

When adhered, the knots do not move over time, that is to say:

(4.11)\[ \ left [{A} ^ {\ text {a}}}\ right]\ mathrm {.} (\ left\ {{u} _ {i}\ right\}\ right\}\ mathrm {-}\ left\ {{u} _ {i\ mathrm {-} 1}\ right\})\ mathrm {=} 0\]

\(\left[{A}^{\text{a}}\right]\) is the matrix of the nodes in adherent contact, i.e. the subpart of the friction matrix \(\left[{A}^{\text{f}}\right]\) (see § 3.5.1) applied to the nodes in adherent contact.

4.3.1.4. Sliding conditions

Shear stress \(\left\{{r}_{i}\right\}\) is collinear to the tangent direction of sliding, i.e.:

(4.12)\[ \ left [{A} ^ {\ text {g}}}\ right]\ mathrm {.} (\ left\ {{u} _ {i}\ right\}\ right\}\ mathrm {-}\ left\ {{u} _ {i\ mathrm {-} 1}\ right\})\ mathrm {})\ mathrm {=}\ mathrm {=}\ mathrm {=}\ lambda\ mathrm {.} \ left\ {{r} _ {i}\ right\}\]

\(\left[{A}^{\text{g}}\right]\) is the matrix of knots in sliding contact, that is, the subpart of the friction matrix \(\left[{A}^{\text{f}}\right]\) (see § 3.5.1) applied to the nodes in sliding contact. We have:

(4.13)\[ \ left [{A} ^ {\ text {g}}}\ right]\ mathrm {.} (\ left\ {\ Delta {u} _ {i} ^ {i} ^ {n\ mathrm {-} 1}\ right\} +\ left\ {\ delta {u} ^ {n}\ right\})\ mathrm {=}\ mathrm {=}\ lambda\ mathrm {.} \ left\ {{r} _ {i} (\ left\ {{u} _ {i}\ right\})\ right\} (\ right\}\]

Equation () depends on the final displacement \(\left\{{u}_{i}\right\}\). The sliding conditions are introduced with a Lagrange multiplier \(\left\{{\mu }^{\text{g}}\right\}\) such as:

(4.14)\[ \ left\ {{\ mu} ^ {\ text {g}}} ({u} _ {i})\ right\}\ mathrm {=}\ mu\ mathrm {.} \ left [=== {\ mu} ^ {\ text {c}} ^ {\ text {c}}} ({u} _ {i}) ===\ right]\ mathrm {.} \ left\ {{t} ^ {n}\ right\}\]

With \({t}^{n}\) the unit vector of the sliding direction which is equal in 3D:

\[\]

: label: eq-62

left{tright}mathrm {=}frac {left [{A} ^ {text {g}}right]mathrm {.} (left{Delta {u} _ {i} ^ {i} ^ {nmathrm {-} 1}right} +left{delta {u} ^ {n}right})} {}right})} {}right{n}rightright{n}rightright}right)} {right})} {right})} {left [{A} ^ {A} ^ {A} ^ {A} ^ {text {g}}right]mathrm {.} (left{Delta {u} _ {i}} ^ {nmathrm {-} 1}right} +left{delta {u} ^ {n}right} ^ {n}right})

Or again:

(4.15)\[ \begin{align}\begin{aligned} \ left\ {{\ mu} ^ {\ text {g}}} ({u} _ {i})\ right\}\ mathrm {=}\ left [{k} ^ {\ text {g}}} ({u} {g}}} ({u} _ {i}) ({u} _ {i})\ right]\ mathrm {.} \ left\ {{t} ^ {n}\ right\}\\ \ textrm {with}\\ \ left [{k} ^ {\ text {g}}} ({u} _ {i})\ right]\ mathrm {=}\ mu\ mathrm {.} \ left [=== {\ mu} ^ {\ text {c}} ^ {\ text {c}} ({u} _ {i}) ===\ right]\end{aligned}\end{align} \]

The Lagrange multiplier is non-linear and depends on the solution \(\left\{{u}_{i}\right\}\) .In 2D, it is alsonon-linear but the multiplier does not depend on the direction of sliding, so we have:

(4.16)\[ {\ left\ {{\ mu} ^ {\ text {g}}} ({u} _ {i})\ right\}} _ {\ text {2D}}\ mathrm {=}}\ mathrm {=}\ mu\ mathrm {.} \ left [=== {\ mu} ^ {\ text {c}}} ({u} _ {i}) ===\ right]\ mathrm {=}\ left [{k} ^ {\ text {g}} {\ text {g}}} ({u} _ {i})\ right]\]

4.3.2. Dualization

In the case of dualization, a trial-and-error algorithm is used which postulates the status of a link a priory and which verifies its condition after applying the Signorini-Coulomb law. To take into account the constraints (we speak of constraints in the sense of « restriction » conditions and not in the mechanical sense of the term) relating to the field of displacement or to the forces, they are brought into the equations through Lagrange multipliers (as can be done in Code_Aster for kinematic boundary conditions). Two sets of Lagrange multipliers are introduced:

• \(\left\{{\mu }^{\text{c}}\right\}\) dealing with contact conditions;

• \(\left\{{\mu }^{\text{g}}\right\}\) dealing with sliding conditions.

By writing the balance of the structure, we give the following interpretation of the Lagrange multipliers:

• \(\left\{{L}_{i}^{\text{c}}({u}_{i})\right\}\mathrm{=}\mathrm{[}{A}^{\text{c}}{\mathrm{]}}^{T}\mathrm{.}\left\{{\mu }_{i}^{\text{c}}\right\}\) represents the nodal forces of contact;

• \(\left\{{L}_{i}^{\text{g}}({u}_{i})\right\}\mathrm{=}\mathrm{[}{A}^{\text{g}}{\mathrm{]}}^{T}\mathrm{.}\left\{{\mu }_{i}^{\text{g}}\right\}\) represents nodal sliding forces.

Even if the friction algorithm uses regularization, we will see that the introduction of « Lagrange multipliers » is necessary to linearize the nodal forces of sliding.

4.3.3. Regularization

The principle of regularization is to modify the laws of touch-friction to obtain ones that are easier to manipulate, for example, for relationships to become univocal and differentiable (to be able to apply Newton’s method for example). Hypotheses are therefore introduced that make the model inaccurate with respect to the Signorini-Coulomb laws.

4.3.3.1. Regularization of contact conditions

The principle of regularization is to modify the graph of the contact law in order to remove the non-univocal nature of the contact relationship.

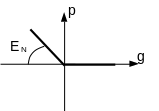
Figure 4.3.3.1-a : regularization of the contact condition (continuous form) .

Remember that the non-interpenetration condition is written in iterative form:

(4.17)\[ \ left [{A} ^ {\ text {c}}}\ right]\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\}\ right\}\ mathrm {\ le}\ left\ {{d} ^ {\ text {c}, n\ mathrm {-} 1}\ right\}\]

The idea of regularization is to penalize the situation for which there is interpenetration. Interpenetration \(\left\{{h}^{n}\right\}\) is worth:

(4.18)\[ \ left\ {{h} ^ {n}\ right\}\ right\}\ mathrm {=}\ left [{A} ^ {\ text {c}}\ right]\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\}\ right\}\ mathrm {-}\ left\ {{d} ^ {\ text {c}, n\ mathrm {-} 1}\ right\} >0\]

In other words, we write that the contact force is greater the greater the greater the interpenetration \(\left\{{h}^{n}\right\}\) is important, hence the regularized form of the contact force:

(4.19)\[ \begin{align}\begin{aligned} {\ left\ {{L} _ {i} ^ {\ text {c} ^ {\ text {c}, n}\ right\}} _ {\ text {regu}}\ mathrm {=} {E} _ {E} _ {N}\ mathrm {.} \ mathrm {[} {A} ^ {\ text {c}} {\ mathrm {]}}} ^ {T}\ mathrm {.} {\ left\ {{h} ^ {n}\ right\}} ^ {\ text {+}}\\ \ textrm {with}\\ {E} _ {N} >0\end{aligned}\end{align} \]

\({E}_{N}\) is the coefficient of regularization (or penalization, of the dimension of a relationship of a force by a displacement) of the contact and \({\square }^{\text{+}}\) is the positive part of a quantity. The contact penalty coefficient is interpreted as the stiffness spring \({E}_{N}\) which opposes the penetration of the slave node into the master surface by applying a corresponding nodal force to it. The bigger it is, the less interpenetration there is and the higher the restoring force.

4.3.3.2. Regularization of the adhesion condition

The principle of the regularization of adhesion is to modify the graph of Coulomb’s law. First, the non-univocal nature of the law in the adherent part is suppressed.

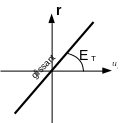
Figure 4.3.3.2-a : regularization of the adhesion condition - Tresca model (continuous form) .

The regulated form of the adhesive force is established:

(4.20)\[ \begin{align}\begin{aligned} {\ left\ {{L} _ {i} ^ {\ text {a} ^ {\ text {a}, n}\ right\}} _ {\ text {regu}}\ mathrm {=} {E} _ {E} _ {T}\ mathrm {.} {\ left [{A} ^ {\ text {a}}}\ right]} ^ {T}\ mathrm {.} \ left [{A} ^ {\ text {a}}}\ right]\ mathrm {.} (\ left\ {\ Delta {u} _ {i} ^ {i} ^ {n\ mathrm {-} 1}\ right\} +\ left\ {\ delta {u} ^ {i} ^ {n}\ right\})\\ \ textrm {with}\\ {E} _ {T} >0\end{aligned}\end{align} \]

\({E}_{T}\) is the coefficient of regularization (or penalization, of the dimension of a relationship of a force by a displacement) of friction. The concept of adherence itself will therefore disappear, all the knots slide. We can see in figure () that this regularization is not satisfactory because we have only transformed the Coulomb problem into a Tresca problem: the force is proportional to the relative sliding. To approach the Coulomb model, one additional inequality must be added:

(4.21)\[\begin{split} \ green {E} _ {T}\ mathrm {.} \ left [{A} ^ {\ text {a}}}\ right]\ mathrm {.} \ left (\ left\ {\ mathrm {\ Delta} {u} {u} _ {i}} ^ {n-1}\ right\} +\ left\ {\ delta {u} ^ {n}\ right\}\ right)\ right\\ right)\ Vert\ le\ mu\ mathrm {.} \ left|p\ left (u\ right)\ right|\end{split}\]

This additional inequality changes the graph (see figure ()). The result is an approximate form of the Coulomb model, in which adherent nodes will be defined in relation to the contact threshold, product of the Coulomb coefficient \(\mu\) and the contact pressure \(p\left(u\right)\). The approximate nature of Coulomb’s law is reflected in the fact that the so-called « adherent » knots will slide all the more when the regularization coefficient is low. The physical interpretation is therefore less direct than in the case of contact, which largely explains the difficulty in finding a satisfactory value of this coefficient in practice. However, the error committed (« false » detection of the sliding threshold) is often not very significant compared to the modeling hypotheses. There is still a non-linearity that concerns the « slippery » part of the law. The treatment of this nonlinearity is reported in § 4.3.4.

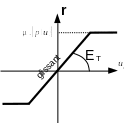
Figure 4.3.3.2-b : regularization of the adhesion condition — Coulomb model (continuous form) .

4.3.4. Slip modeling

The sliding conditions are always introduced with a Lagrange multiplier \(\left\{{\mu }^{\text{g}}\right\}\) which is expressed (in 3D) from ():

(4.22)\[ \ left\ {{\ mu} ^ {\ text {g}}} ({u} _ {i})\ right\}\ mathrm {=}\ left [{k} ^ {\ text {g}}} ({u} {g}}} ({u} _ {i}) ({u} _ {i})\ right]\ mathrm {.} \ left\ {{t} ^ {n}\ right\}\]

This reveals the two unknowns that both depend on the solution: the contact pressure in the sliding threshold matrix \(\left[{k}^{\text{g}}\right]\) and the sliding direction \(\left\{{t}^{\text{n}}\right\}\). In practice, however, it is considered that knowledge of the sliding threshold \(\left[{k}^{\text{g},n\mathrm{-}1}\right]\) is acquired at the previous iteration \((n-1)\), which is equivalent to reducing ourselves to a Tresca criterion for each iteration. At convergence the threshold is obviously fixed: there are therefore no longer any differences between the thresholds during the iterations. \(\left\{{\mu }^{\text{g},n}\right\}\) is therefore approximated to the state of the previous iteration \((n-1)\):

\[\]

: label: eq-71

left{{mu} ^ {text {g}, n}right}right}mathrm {approx}left [{k} ^ {text {g}, nmathrm {-}} 1}right]mathrm {.} frac {left [{A} ^ {text {g}}right]mathrm {.} (left{Delta {u} _ {i} ^ {i} ^ {nmathrm {-} 1}right} +left{delta {u} ^ {n}right})} {}right})} {}right{n}rightright{n}rightright}right)} {right})} {right})} {left [{A} ^ {A} ^ {A} ^ {A} ^ {text {g}}right]mathrm {.} (left{Delta {u} _ {i} ^ {i} ^ {nmathrm {-} 1}right} +left{delta {u} ^ {n}right})}mathrm {=}mathrm {=} ^}left [{k}} ^ {k} ^ {text {g}, nmathrm {-} 1}right]mathrm {=}left {=}left [{k} ^ {k} ^ {g}, nmathrm {-} 1}right]mathrm {.} left{{t} ^ {n}right}

We also have the sliding threshold from the previous iteration:

(4.23)\[ \ left [{k} ^ {\ text {g}, n\ mathrm {-} 1}\ right]\ mathrm {=}\ mu\ mathrm {.} \ left [=== {\ mu} ^ {\ text {c} ^ {\ text {c}, n\ mathrm {-} 1} ===\ right]\]

4.3.5. Linearizations

To solve the non-linear problem, it is necessary to linearize the quantities that depend on \(\left\{{u}_{i}^{n}\right\}\) in the equilibrium equation (). Writing contact/friction forces introduces non-linear quantities that must therefore be linearized in order to be able to apply Newton’s algorithm. In the following table, the cases where linearization is necessary are listed according to the type of algorithm.

	Dualization	Regularization
\(\left\{{L}_{i}^{\text{c},n}\right\}\)	No linearization	Linearization
\(\left\{{L}_{i}^{\text{a},n}\right\}\)		Linearization
\(\left\{{L}_{i}^{\text{g},n}\right\}\)		Linearization

4.3.5.1. Linearization of contact forces

We regularize the contact condition from the expression () for the contact force, when we are in the interpenetration phase, that is to say by assuming \(\left\{{h}^{n}\right\}>0\):

(4.24)\[ {\ left\ {{L} _ {i} ^ {\ text {c} ^ {\ text {c}, n}\ right\}} _ {\ text {regu}}\ mathrm {=} {E} _ {E} _ {N}\ mathrm {.} \ mathrm {[} {A} ^ {\ text {c}} {\ mathrm {]}}} ^ {T}\ mathrm {.} (\ left [{A} ^ {\ text {c}}}\ right]\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\} {n}\ right\}\ mathrm {-}\ left\ {{d} ^ {\ text {c}, n\ mathrm {-} 1}\ right\})\]

By linearizing, we obtain:

(4.25)\[\begin{split} {\ left\ {{L} _ {i} ^ {\ text {c} ^ {\ text {c}, n}\ right\}} _ {\ text {regu}}\ underset {\ text {linearization}} {\ to} {\ left\\ left\ {\ left\ left\ {\ left\ {\ left\ {c}} ^ {\ text {regu}}} {\ text {linearization}}} {\ to} {\ left} {\ left\ left\ left\ {\ left\ {\ left\ {\ left\ {\ stackrel {c}} ^ {\ text {regu}}} _ {\ text {regu}} _ {\ text {regu}}}\ mathrm {=}\ mathrm {[} {K}} _ {i} ^ {\ text {c}, n\ mathrm {-} 1}\ mathrm {]}}\ mathrm {]}\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\} ^ {n}\ right\}} +\ left\ {{L} _ {i} ^ {\ text {c}, n\ mathrm {-} 1}\ right\}\end{split}\]

\(\mathrm{[}{K}_{i}^{\text{c},n\mathrm{-}1}\mathrm{]}\) makes a new contribution to the tangent matrix of the problem, it is the tangent « contact » matrix. It is obviously worth:

(4.26)\[ \ mathrm {[} {K} _ {i} ^ {i} ^ {\ text {c}, n\ mathrm {-} 1}\ mathrm {]}\ mathrm {=} {E} {E} _ {E} _ {N}\ mathrm {.} \ mathrm {[} {A} ^ {\ text {c}, n\ mathrm {-} 1} {\ mathrm {]}}} ^ {T}\ mathrm {.} \ mathrm {[} {A} ^ {\ text {c}, n\ mathrm {-} 1}\ mathrm {]}}\]

And \(\left\{{L}_{i}^{\text{c},n\mathrm{-}1}\right\}\) contributes to the second member, it is worth:

(4.27)\[ \ left\ {{L} _ {i} ^ {\ text {c}, n\ mathrm {-} 1}\ right\}\ mathrm {=}\ mathrm {-} {E} {E} _ {N}\ mathrm {.} \ mathrm {[} {A} ^ {\ text {c}, n\ mathrm {-} 1} {\ mathrm {]}}} ^ {T}\ mathrm {.} \ left\ {{d} ^ {\ text {c}, n\ mathrm {-} 1}\ right\}\]

It should be noted that the contact penalty coefficient is interpreted as the spring of stiffness \({E}_{N}\) which opposes the penetration of the slave node into the master surface. The larger it is, the less interpenetration there is and the higher the restoring force, but this coefficient also intervenes in the tangent matrix, which changes its conditioning and makes the resolution of the linear system more difficult. When the contact is not activated (i.e. if \(\left\{{h}^{n}\right\}\mathrm{\le }0\)), the matrix and the second member vector are zero.

4.3.5.2. Linearization of adhesive forces

We regularize the adhesion condition from the expression () of the adhesive force, when we are in the adhesion phase (in the sense defined in § 4.3.3.2), that is to say by assuming that the inequality () is strictly respected:

(4.28)\[ {\ left\ {{L} _ {i} ^ {\ text {a} ^ {\ text {a}, n}\ right\}} _ {\ text {regu}}\ mathrm {=} {E} _ {E} _ {T}\ mathrm {.} {\ left [{A} ^ {\ text {a}}}\ right]} ^ {T}\ mathrm {.} \ left [{A} ^ {\ text {a}}}\ right]\ mathrm {.} (\ left\ {\ Delta {u} _ {i} ^ {i} ^ {n\ mathrm {-} 1}\ right\} +\ left\ {\ delta {u} ^ {i} ^ {n}\ right\})\]

By linearizing, we obtain:

(4.29)\[\begin{split} {\ left\ {{L} _ {i} ^ {\ text {a} ^ {\ text {a}, n}\ right\}} _ {\ text {regu}}\ underset {\ text {linearization}} {\ to} {\ left\\ left\ {\ left\ left\ {\ left\ {\ left\ a} ^ {\ text {regu}}} {\ text {linearization}}} {\ to} {\ left\ left\ left\ {\ left\ {\ left\ {\ left\ {\ stackrel {a}, n} {\ text {linearization}} {\ left} {\ left\ left\ {\ left\ {\ left\ {\ stackrel {a}, n} {\ text {regu}}}\ mathrm {=}\ mathrm {[} {K}} _ {i} ^ {\ text {a}, n\ mathrm {-} 1}\ mathrm {]}}\ mathrm {]}\ mathrm {.} \ left\ {\ delta {u} ^ {n}\ right\} ^ {n}\ right\}} +\ left\ {{L} _ {i} ^ {\ text {a}, n\ mathrm {-} 1}\ right\}\end{split}\]

\([{K}_{i}^{\text{a},n-1}]\) makes a new contribution to the tangent matrix of the problem, it is the tangent « adherence » matrix. It is obviously worth:

(4.30)\[ [{K} _ {i} ^ {\ text {a}, n-1}] = {E} _ {T\ mathrm {.}} [{A} ^ {\ text {a}, n-1} {]} {]} ^ {T\ mathrm {.}} [{A} ^ {\ text {a}, n-1}]\]

And \(\left\{{L}_{i}^{\text{a},n-1}\right\}\) contributes to the second member, it is worth:

(4.31)\[ \ left\ {{L} _ {i} ^ {\ text {a}, n-1}\ right\} = {E} _ {T\ mathrm {.}} [{A} _ {\ text {a}}} ^ {n-1} {]} ^ {T\ mathrm {.}} \ left\ {\ mathrm {\ Delta} {u} {u} _ {i} ^ {n-1}\ right\}\]

It should be noted that the contact penalty coefficient is interpreted as the spring of stiffness \({E}_{T}\) (with the dimension of a relationship of a force by a displacement) which opposes the relative sliding of the two surfaces. The larger it is, the greater the restoring force, but this coefficient also intervenes in the tangent matrix, which changes its conditioning and makes it more difficult to solve the linear system.

4.3.5.3. Linearization of sliding forces

We saw in § 4.3.4 that the sliding forces depended on the final displacement \(\left\{{u}_{i}\right\}\) by the Tresca threshold, but that we assumed that the information at iteration \((n\mathrm{-}1)\) was sufficient to solve Coulomb’s law [biB6] _, [bib13] _ by writing:

\[\]

: label: eq-81

left{{mu} ^ {text {g}, n}right} =left [{k} ^ {text {g}, n-1}right]mathrm {.} left{{t} ^ {n}right}

However, you should prepare for what will happen in the next iteration \((n+1)\) if the threshold is not correct and will require a new iteration. In Newton’s next iteration, the displacement solution will be:

\[\]

: label: eq-82

left{{u} _ {i} ^ {n+1}right+1}right}right}left{{u} _ {imathrm {-} 1}right} +right} +left{Delta {n+1}} +left{delta {u}}right}mathrm {=}left{{u} _ {imathrm {-} 1}right} 1}right} +left{Delta {u} _ {i} ^ {nmathrm {-} 1}right1}right} 1}right} +left{delta {u}} ^ {n+1}right} +left{delta {u} ^ {n+1}right} +left{delta {u} ^ {n+1}right}

It is therefore necessary to linearize the quantity () in \((n+1)\):

\[\]

: label: eq-83

left{{mu} ^ {text {g}, n+1}right}mathrm {=}left [{k} ^ {text {g}, n}, n}right]mathrm {.} left{tright}

Equation () is of the form \(\frac{\left\{h({x}^{n+1})\right\}}{∥\left\{h({x}^{n+1})\right\}∥}\) with \(\left\{{x}^{n+1}\right\}\mathrm{=}\left\{{x}^{n}\right\}+\left\{{\delta x}^{n+1}\right\}\). Linearization is written as:

(4.32)\[ \ left [k\ right]\ mathrm {.} \ frac {\ left\ {h ({x} ^ {n+1})\ right\}} {\ left\ {h ({x} ^ {n+1})\ right\}}\ underset {\ text {linearization}}\ underset {\ text {linearization}} {\ text {linearization}} {\ to}\ left [k\ right]\ mathrm {.}}\ underset {\ text {linearization}}} {\ text {linearization}} {\ to}\ left [k\ right]\ mathrm {.} (\ frac {\ left\ {h ({x} ^ {n})\ right\ {n})\ right\}} {b>\ left\ {h ({x} ^ {n})\ right\}}} +\ frac {1} {1} {{1} {{1} {{{n}} +\ frac {1} {} {{1} {{{n}} +\ frac {1} {} {{1} {} {{n})\ left\ {h ({x} ^ {n})\ right\ {x} ^ {n})\ right\ {x} ^ {n}) +\ frac {1} {1} (\ left [I\ right]\ mathrm {-}\ frac {\ left\ {h ({x} ^ {n})\ right\}\ langle\ left\ {h ({x} ^ {n})\ right\} ^ {n})\ right\} ^ {n})\ right\} ^ {n})\ right\} ^ {n})\ mathrm {.} \ left\ {\ delta {x} ^ {n+1}\ right\})\]

We apply () to the expression () with:

(4.33)\[ \begin{align}\begin{aligned} \ left\ {{x} ^ {n}\ right\}\ right\}\ leftarrow\ left\ {\ Delta {u} _ {i} ^ {n\ mathrm {-} 1}\ right\} 1}\ right\} +\ right\} +\ right\} +\ left\ {\ right\} +\ left\ {\ delta {u}\ left\\ \ textrm {and}\\ \ left\ {{x} ^ {n+1}\ right\}\ right\}\ leftarrow\ left\ {\ Delta {u} _ {i} ^ {n\ mathrm {-} 1}\ right\}\ right\} +\ left\ {n+1}\ right\} +\ left\ {\ delta {u} ^ {n+1}\ right\} +\ left\ {\ delta {u} ^ {n+1}\ right\}\\ \ left\ {{\ delta x} ^ {n+1}\ right\}\ leftarrow\ left\ {\ delta {u} ^ {n+1}\ right\}\\ \ left\ {h ({x} ^ {n})\ right\}\ right\}\ leftarrow\ left [{A} ^ {\ text {g}}\ right]\ mathrm {.} (\ left\ {\ Delta {u} _ {i} ^ {i} ^ {n\ mathrm {-} 1}\ right\} +\ left\ {\ delta {u} ^ {i} ^ {n}\ right\})\\ \ textrm {and}\\ \ left\ {h ({x} ^ {n+1})\ right\}\ right\}\ leftarrow\ left [{A} ^ {\ text {g}}\ right]\ mathrm {.} (\ left\ {\ Delta {u} _ {i}} ^ {n\ mathrm {-} 1}\ right\} +\ left\ {\ delta {u} ^ {n}\ right\} +\ left\ {i}\ right\} ^ {\ delta {u} ^ {n+1}\ right\})\\ \ left [k\ right]\ leftarrow\ left [{k} ^ {\ text {g}, n}\ right]\end{aligned}\end{align} \]

We linearize ():

(4.34)\[ \ left\ {{\ mu} ^ {\ text {g}, n+1}, n+1}\ right\}\ underset {\ text {linearization}} {\ to}\ left\ {{\ stackrel {}} {} {\ mu}}} ^ {\ text {g}, n+1}\ right\}\]

We start by noting \(\left\{{g}^{\text{t},n}\right\}\) the tangential slippage relating to iteration \(n\):

(4.35)\[ \ left\ {{g} ^ {\ text {t}, n}\ right\}\ right\}\ mathrm {=}\ left [{A} ^ {\ text {g}}}\ right]\ right]\ mathrm {.} (\ left\ {\ Delta {u} _ {i} ^ {i} ^ {n\ mathrm {-} 1}\ right\} +\ left\ {\ delta {u} ^ {i} ^ {n}\ right\})\]

We get:

\[\]

: label: eq-88

left{{stackrel {} {mu}}} ^ {text {g}}} ^ {text {g}, n+1}right}mathrm {=}left [{k} ^ {text {g} ^ {text {g}, n}right]mathrm {.} (frac {left{{g} ^ {text {t}} ^ {text {t}, n}right}} {left{{g} ^ {text {t}, n}right}}right}right}, {{g} ^ {text {t}} ^ {text {{g}} ^ {text {t}, n}right}, n}right}right} (left [Iright]mathrm {-}frac {left{{g}} ^ {text {t}, n}right}langle {g} ^ {text {t}, n}rangle}rangle} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{}} {{g} ^ {g} ^ {g} ^ {g} ^ {g} ^ {g} ^ {2}})mathrm m {.} left{delta {u} ^ {n+1}right})

If we note:

(4.36)\[ \ left\ {{\ rho} ^ {\ text {g}, n}\ right}\ mathrm {=}\ left [{k} ^ {\ text {g}, n}, n}\ right]\ mathrm {.} \ frac {\ left\ {{g} ^ {\ text {t}} ^ {\ text {t}, n}, n} {\ text {t}, n} {\ text {t}, n}\ right {t}, n}\ right\}\]

And:

(4.37)\[ \ left [{B} ^ {\ text {g}, n}, n}\ right]\ mathrm {=}\ frac {\ left [{k} ^ {\ text {g}, n}\ right]} {{\ text {g}, n} {\ text {g}, n}\ right\ {k} ^ {\ text {g}, n}\ right\},\ mathrm {.} (\ left [I\ right]\ mathrm {-}\ frac {\ left\ {{g}} ^ {\ text {t}, n}\ right\}\ langle {g} ^ {\ text {t}, n}, n}\ rangle} {{rangle}}\ rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{2}} {{2}})\]

We can write () in the following condensed form:

\[\]

: label: eq-91

left{{stackrel {} {mu}}} ^ {text {g}}} ^ {text {g}, n+1}right}mathrm {=}left [{B} ^ {text {g} ^ {text {g}, n}right]mathrm {.} left{delta {u} ^ {n+1}right}right} +left{{rho} ^ {text {g}, n}right}

The sliding force is expressed as a function of the Lagrange multiplier:

\[\]

: label: eq-92

left{{L} _ {i} ^ {text {g} ^ {text {g}, n+1}right}mathrm {=} {left [{A} ^ {text {g}}}right}right]}right]} ^ {T}mathrm {.} left{{mu} ^ {text {g}, n+1}right}

Since matrix \(\left[{A}^{\text{g}}\right]\) does not depend on the displacement, the linearized sliding force can be written as:

(4.38)\[ \ left\ {{L} _ {i} ^ {\ text {g} ^ {\ text {g}, n+1}\ right\}\ underset {\ text {linearization}} {\ to}\ left\ {{\ stackrel {} {L} {L}} {L}}} {\ l}} {L}} {L}} {L}} {L}} {L}} {L}} {L}} {L}} {L}}} _ {i}}} _ {i}}} _ {i}} ^ {i} ^ {\ text {g}, n+1}\ right\}\ mathrm {=} {\ left [{A}} {\ left [{A}} {L} {L} {L} {L}} {L}} g}}\ right]} ^ {T}\ mathrm {.} \ left\ {{\ stackrel {} {\ mu}}} ^ {\ text {g}}} ^ {\ text {g}, n+1}\ right\}\ mathrm {=}\ left [{K} ^ {\ text {g} ^ {\ text {g}, n}\ right]\ mathrm {.} \ left\ {\ delta {u} ^ {n+1}\ right\} +\ left\ {{L} ^ {\ text {g}, n}\ right\}\]

With the \(\left[{K}^{\text{g},n}\right]\) sliding matrix such as:

(4.39)\[ \ left [{K} ^ {\ text {g}, n}\ right]\ right]\ mathrm {=} {\ left [{A} ^ {\ text {g}}\ right]}\ right]} ^ {T}\ mathrm {.} \ left [{B} ^ {\ text {g}, n}\ right]\]

And the vector:

(4.40)\[ \ left\ {{L} ^ {\ text {g}, n}\ right\}\ right\}\ mathrm {=} {\ left [{A} ^ {\ text {g}}\ right]}\ right]} ^ {T}\ mathrm {.} \ left\ {{\ rho} ^ {\ text {g}, n}\ right\}\]

\(\left[{K}^{\text{g},n}\right]\) makes a new contribution to the tangent matrix of the problem, it is the tangent « sliding » matrix. It is obviously worth:

(4.41)\[ \ left [{K} ^ {\ text {g}, n}\ right]\ mathrm {=}\ frac {{\ left [{A} ^ {\ text {g}}\ right]}\ right]}} ^ {T}\ mathrm {.} \ left [{k} ^ {\ text {g}, n}, n}\ right]} {\ left\ {{g} ^ {\ text {t}, n}\ right\}, n}\ right\} (\ left [I\ right]\ mathrm {-}\ frac {\ left\ {{g}} ^ {\ text {t}, n}\ right\}\ langle {g} ^ {\ text {t}, n}, n}\ rangle} {{rangle}}\ rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{rangle}} {{2}} {{2}})\]

The second part of the expression is preceded by the sign \(\mathrm{-}\), the effect of this contribution is particularly destabilizing for the overall behavior of the matrix tangent to the system, more particularly when one is far from equilibrium and therefore at the beginning of the resolution at each new time step. We therefore decide to take it into account only partially by assigning it a coefficient \(\theta \in [\mathrm{0,1}]\) that can be modified using the COEF_MATR_FROT keyword:

(4.42)\[ \ left [{\ tilde {K}} _ {\ theta}} ^ {\ text {g}, n}\ right]\ mathrm {=}\ frac {{\ left [{A} ^ {\ text {a} ^ {\ text {g}} ^ {g}} ^ {g}\ mathrm {.} \ left [{k} ^ {\ text {g}, n}, n}\ right]} {\ left\ {{g} ^ {\ text {t}, n}\ right\}, n}\ right\} (\ left [I\ right]\ mathrm {-}\ theta\ mathrm {.} \ frac {\ left\ {{g} ^ {\ text {t} ^ {\ text {t}, n}\ right\}\ langle {g} ^ {\ text {t}, n}\ rangle} {{\ left\ {{g}} ^ {\ text {g}} ^ {{g}} ^ {{g}} ^ {{g}} ^ {{g}} ^ {{g}} ^ {{g} ^ {{g} ^ {\ text {t}, n}\ right\},\]

It is recommended to use an initial value of \(0.5\) for this coefficient and to reduce it if convergence is not obtained. In the case where \(\theta =0\) convergence seems to still be achieved but is particularly slow. When one is close to the solution, on the other hand, it is very useful to have a value of this coefficient equal to \(1\) in order to accelerate convergence. This is done automatically in the code when residue RESI_GLOB_RELA is less than \({10}^{-3}\). Replace \(\left[{K}^{\text{g},n}\right]\) with \(\left[{\tilde{K}}_{\theta }^{\text{g},n}\right]\).

The second member is finally worth:

(4.43)\[ \ left\ {{L} ^ {\ text {g}, n}\ right\}\ right\}\ mathrm {=} {\ left [{A} ^ {\ text {g}}\ right]}\ right]} ^ {T}\ mathrm {.} \ left [{k} ^ {\ text {g}, n}\ right]\ mathrm {.} \ frac {\ left\ {{g} ^ {\ text {t}} ^ {\ text {t}, n}, n} {\ text {t}, n} {\ text {t}, n}\ right {t}, n}\ right\}\]

In 2D, the Lagrange multiplier for sliding is approximated by:

(4.44)\[ {\ left\ {{\ mu} ^ {\ text {g}}} ({u} _ {i})\ right\}} _ {\ text {2D}}\ mathrm {=}}\ mathrm {=}\ mu\ mathrm {.} \ left [=== {\ mu} ^ {\ text {c}}} ({u} _ {i}) ===\ right]\ mathrm {=}\ left [{k} ^ {\ text {g}} {\ text {g}}} ({u} _ {i})\ right]\]

We can demonstrate \({\left[{K}^{\text{g},n}\right]}_{\text{2D}}\mathrm{=}0\). And so:

\[\]

: label: eq-100

{left{stackrel {} {L}}} _ {i}}} _ {i}} ^ {text {g}, n+1}right}} _ {text {2D}}mathrm {=}} {=} {left} {left [{A}} ^ {A} ^ {text {g}}right]} ^ {T}mathrm {.} left{{rho} ^ {text {g}, n}right}

4.3.6. General algorithms

Discrete methods for solving the touch/friction problem are based on an decouple approach between balance and touch/friction. Contact/friction (noted \(C\) in the second column) is treated after each Newton’s iteration of the global problem (noted \(G\) in the second column).

Without taking contact into account, we will note the solution vectors with a \(\text{~}\), for example:

\[\]

: label: eq-101

left{{tilde {u}} _ {i}} _ {i} ^ {n}right}mathrm {=}left{{u} _ {imathrm {-} 1}right}right}}}right}right}right}right}}right}right}right}right}}right}right}}right}}right}right}}right}right}}right}}right}right}}right}}right}right}}right}}right}right}}right}}right}right}}right} {u}} ^ {n}right}

4.3.6.1. The case of dualization

The general procedure for the dualized case is as follows:

At the Newton iteration \(n\)
1	G	Solving the balance problem without contact, equation ()	\(\to \left\{\delta {\tilde{u}}^{n}\right\}\)
2	G	Contactless travel update	\(\left\{{\tilde{u}}_{i}^{n}\right\}\mathrm{=}\left\{{u}_{i\mathrm{-}1}\right\}+\left\{\Delta {u}_{i}\right\}+\left\{\delta {\tilde{u}}^{n}\right\}\)
3	C	Modification of trips to respect contact conditions	\(\left\{\delta {\tilde{u}}^{n}\right\}\to \left\{\delta {u}^{n}\right\}\)
4	C	Update of trips with contact taken into account	\(\left\{{u}_{i}^{n}\right\}\mathrm{=}\left\{{u}_{i\mathrm{-}1}\right\}+\left\{\Delta {u}_{i}^{n\mathrm{-}1}\right\}+\left\{\delta {u}^{n}\right\}\)
5	C	Calculation of contact forces	\(\left\{{L}_{i}^{\text{c},n}\right\}\) and \(\left\{{L}_{i}^{\text{f},n}\right\}\)
6	C	Possible calculation of matrices (case of sliding)	\(\left[{K}^{\text{g},n+1}\right]\)
7	G	Calculation of internal and external forces with modified displacements	\(\left\{{L}_{i}^{\text{ext},n}\right\}\) and \(\left\{{L}_{i}^{\text{int},n}\right\}\)
8	G	Balance check

The \(\left[{K}^{\text{cf},n+1}\right]\) matrix is only calculated in the case of slippage. It will not necessarily be used, everything will depend on Newton’s convergence and on the contact/friction algorithm (Tresca threshold converged on the Coulomb problem).

4.3.6.2. The case of regularization

The general procedure for the regularized case (penalization) is as follows:

At the Newton iteration \(n\)
1	G	Solving the balance problem without contact, equation ()	\(\to \left\{\delta {\tilde{u}}^{n}\right\}\)
2	G	Contactless travel update	\(\left\{{\tilde{u}}_{i}^{n}\right\}\mathrm{=}\left\{{u}_{i\mathrm{-}1}\right\}+\left\{\Delta {u}_{i}^{n\mathrm{-}1}\right\}+\left\{\delta {\tilde{u}}^{n}\right\}\)
3	C	Calculation of touch/friction forces	\(\left\{{L}_{i}^{\text{c},n}\right\}\) and \(\left\{{L}_{i}^{\text{f},n}\right\}\)
4	C	Calculation of modified matrices	\(\left[{K}^{\text{cf},n+1}\right]\)
5	G	Calculation of internal and external forces	\(\left\{{L}_{i}^{\text{ext},n}\right\}\) and \(\left\{{L}_{i}^{\text{int},n}\right\}\)
6	G	Balance check

The touch/friction algorithm does not modify the movements, it is the global system that will modify them. This implies that for penalized methods, we will always need at least two Newton iterations, even in the elastic case: one iteration to solve the balance problem without contact/friction and a second iteration to integrate the touch-friction conditions that will modify the global system.

[1]

There are several ways to choose and calculate this matrix. For more details see [R5.03.01]

[2]

The idea of transforming the Coulomb problem into a succession of Tresca problems is very largely justified in the literature (see for example) and mostly used in commercial codes. It is also the strategy used in the « fixed point » version of the algorithm in continuous formulation (see [R5.03.52]).