1. Introduction#

Idriss and Seed (1967) [1] were the first to propose an equivalent linear approach for the analysis of site response to seismic stress. Later, Schnabel et al. (1972) [2] implemented this method in the frequency domain with the SHAKE program. The equivalent linear method has since been implemented in several calculation codes (SHAKE, FLUSH,,,,, CYBERQUAKE, DEEPSOIL, EERA,…) and in code_aster under the operator DEFI_SOL_EQUI, [U4.84.31].

This method is suitable for evaluating the response of ground profiles made up of horizontal layers subjected to the vertical propagation of seismic waves. A 1D modeling — One component considers only the propagation of shear waves in a horizontal direction, while a 1D modeling — Three components considers the vertical propagation of three plane waves (SV, SH and P).

In fact, the ground can in practice be considered to be linear viscoelastic for distortions that satisfy \(\mathrm{\gamma }=2{\mathrm{\epsilon }}_{\mathit{xz}}\le \mathrm{1,0}\times {10}^{-5}\). For higher distortions, the behavior of the soil is described by experimental curves giving the variation of the shear modulus \(G\) and of the critical damping percentage \(D\) as a function of the distortion (noted gamma \(\gamma =2{\varepsilon }_{\mathrm{xz}}\)) (see figure). it is accepted that this approach is acceptable up to distortions verifying: \(\mathrm{\gamma }=2{\mathrm{\epsilon }}_{\mathit{xz}}\le \mathrm{1,0}\times {10}^{-3}\). beyond that, it is appropriate to use a nonlinear behavior model coupling dilatance and distortions.

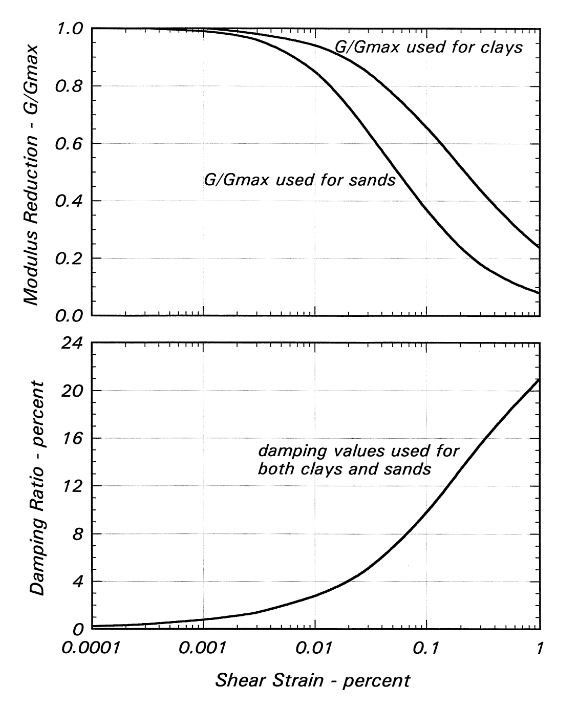
Figure 1-1Example of G/Gmax-Gamma and D-Gamma curve [9].

As a reminder, the shear modulus \(G\) is linked to the Young modulus \(E\) and to the speed of the shear waves \({V}_{s}\) by the following formula:

(1.1)#\[ G=\ frac {E} {2 (1+\ mathrm {\nu})} =\ mathrm {\ rho}\ mathrm {.} {{V} _ {s}}} ^ {2}\]

With \(\mathrm{\rho }\) the density, and \(\nu\) the Poisson’s ratio.