4. Formulations of equivalent linear behavior#
4.1. Schnabel formulation#
Schnabel et al. (1972) [2] relate viscosity to the damping of material \(D\), by \(H\omega =2\mathrm{GD}\). The critical damping of material \(D\) is the value measured in the laboratory and transferred to the \(D\) -gamma curves.
The complex shear modulus is then written as:
The stiffness \(G\) is taken to be equal to the secant module \({G}_{s}\) of the curves (\({\sigma }_{\mathrm{xz}}-\gamma\)) (see). The value of the complex shear modulus is equal to:
The modulus of the complex shear modulus \(∣{G}^{\ast }∣\) and \(D\) therefore increase jointly. The represents the value of \(\frac{∣{G}^{\ast }∣}{G}\) as a function of \(D\). For example, for a damping coefficient \(D\) reduced by 20%, the modulus of the complex shear modulus is 8% greater than the value of \(G\).
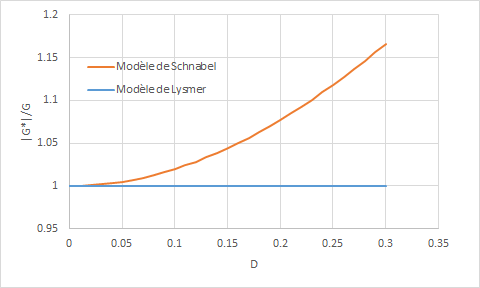
Figure4.1-1. Evolution of \(\frac{∣{G}^{\ast }∣}{G}\) as a function of \(D\) for the Schnabel model, compared to that for the Lysmer model.
To solve this problem, Lysmer formulated a second equivalent linear model.
4.2. Lysmer formulation#
Lysmer’s formulation consists in rewriting the complex shear modulus \({G}^{\ast }\) to ensure that the \(\frac{∣{G}^{\ast }∣}{G}\) ratio is always equal to one. The complex shear modulus is then written as:
The energy dissipated in a cycle is then:
4.3. Comparison of the energies dissipated by the two formulations#
The figure shows that the complex shear modulus \(∣{G}^{\ast }∣\) is overvalued with the Schnabel formulation, and rigorously equal to \(G\) for the Lysmer formulation. The energy dissipated during a charging cycle is also compared between the two formulations as a function of \(D\).
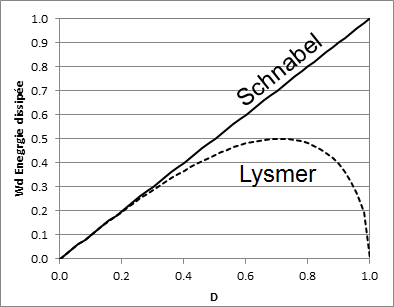
Figure 4.3-1: Comparison of the energy dissipated during a loading cycle for the two formulations of the equivalent linear as a function of damping \(D\) [5].
The energy dissipated between the two formulations is the same until around \(D=\mathrm{0,2}\), then the Lysmer formulation dissipates less energy. The domain of validity of the equivalent linear model means that the domain of interest of these curves is on the interval \([\mathrm{0,}0.3]\). We then notice that even though \({D}_{\mathit{Schnabel}}<{D}_{\mathit{Lysmer}}\), the Schnabel model can dissipate more energy than the Lysmer model.