9. Static problem#
This problem is that of seeking the balance of a cable structure in any position and subject to a system of given forces.
9.1. Iterative algorithm#
The equilibrium equation, the discretized form of [eq] and [eq] without the inertia term, which must be satisfied at each node, is:
\({F}_{\text{int}}={F}_{\text{ext}}\) [10]
Suppose we’ve just calculated the cable displacement field, \({u}^{n}({s}_{o})\), in iteration \(n\):
if this field makes it possible to satisfy, with one tolerance, [éq 9.1-1], the line is considered to be:
\(x({s}_{o})+{u}^{n}({s}_{o})\)
is the balance figure of the cables;
otherwise, displacement corrections \(\Delta {u}^{n+1}\) are calculated by the linearized system:
\(\left[{K}_{M}^{n}+{K}_{G}^{n}\right]\Delta {u}^{n+1}={F}_{\text{ext}}-{F}_{\text{int}}^{n}\)
For this purpose, the nonlinear, quasistatic algorithm described in [R5.03.01] is used, and which corresponds to the STAT_NON_LINE command. The move in iteration \((n+1)\) is:
\({u}^{n+1}={u}^{n}+\Delta {u}^{n+1}\)
We see if [eq] is satisfied by field \({u}^{n+1}\) and so on.
9.2. example#
We want to calculate the equilibrium figure of a heavy cable [fig 9.2-a] whose one end \(A\) is fixed and whose other end, \(B\) at level with \(A\), is subject to a given horizontal force.
This problem is addressed in [bib], where it is considered to be highly nonlinear.
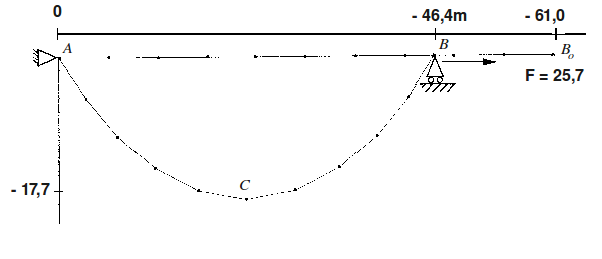
Extensional stiffness (E.A): 4.45 x 105 N, Line weight: 1.46 N/m
Figure 2: Balance of a heavy cable subjected to horizontal tension
Initially, the cable, modelled by 10 elements of the 1st degree, is assumed to be weightless and has a rectilinear horizontal position \({\mathrm{AB}}_{o}\). It is simultaneously subjected to the action of gravity and to the horizontal force \(F\) applied in \({B}_{o}\). Static equilibrium position \(\mathrm{ACB}\) is reached in only 8 iterations.