1. Reference problem

1.1. Geometry

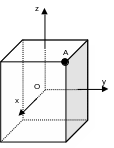
Cube geometry:

Center \(O(0.\mathrm{,0}\mathrm{.}\mathrm{,0}\mathrm{.})\)

Point \(A(0.5\mathrm{,0}.5\mathrm{,0}.5)\)

Side cube \(1m\)

1.2. Material properties

• • • Elastic

      • \(E=5800.0\mathrm{E6}\mathrm{Pa}\) Young’s module

      • \(\rho =2500{\mathrm{kg.m}}^{-3}\) Density

      • \(\nu =0.3\) Poisson’s ratio

• • • DRUCK_PRAGER with linear negative work hardening

      • \(\alpha =0.33\) Pressure Dependence Coefficient

      • \({p}_{\mathrm{ultm}}=0.01\) Ultimate cumulative plastic deformation

      • \({\sigma }^{Y}=2.57\mathrm{E6}\mathrm{Pa}\) Plastic constraint

      • \(h=-2.00\mathrm{E8}\mathrm{Pa}\) Work hardening module

• • • DRUCK_PRAGER with parabolic negative work hardening

      • \(\mathrm{\alpha }=0.33\) Pressure Dependence Coefficient

      • \({p}_{\mathit{ultm}}=0.01\) Ultimate cumulative plastic deformation

      • \({\mathrm{\sigma }}^{Y}=2.57E6\mathit{Pa}\) Plastic constraint

• • • • \({\mathrm{\sigma }}_{\mathit{ultm}}^{Y}=0.57E6\mathit{Pa}\) Ultimate constraint

    • DRUCK_PRAG_N_A with parabolic negative work hardening

      • \(\alpha =0.33\) Pressure Dependence Coefficient

      • \({p}_{\mathrm{ultm}}=0.01\) Ultimate cumulative plastic deformation

      • \({\sigma }^{Y}=2.57\mathrm{E6}\mathrm{Pa}\) Plastic constraint

      • \({\sigma }_{\mathrm{ultm}}^{Y}=0.57\mathrm{E6}\mathrm{Pa}\) Ultimate constraint

      • \(\mathrm{\beta }=0.33\) Initial expansion coefficient

• • • Hydraulic behavior: saturated liquid

• • • • \(\mathrm{Pre1}=1\mathrm{Pa}\) Reference liquid pressure

      • \({\rho }_{\mathrm{pre1}}=1000{\mathrm{kg.m}}^{-3}\) Density of water

      • \(\mathrm{Poro}=0.14\) Initial porosity

      • \({\rho }_{\mathrm{vh}}=2400{\mathrm{kg.m}}^{-3}\) Homogenized density

      • \(\mathrm{bio}=1\) Biot coefficient

      • \({K}_{\mathrm{intrinsèque}}=1E-18{m}^{2}\) Intrinsic permeability

      • \(\frac{1}{{K}_{l}}=0\) Incompressible liquid

      • \(\mathrm{vi}=1.0E-3\mathrm{Pa.s}\) Viscosity

1.3. Boundary conditions and loads

Boundary conditions and loads are applied in two steps:

• Step \(A\): \(t\in [\mathrm{0,1}\mathrm{.}]\)

Boundary conditions

• • Knot pressure \(\mathrm{PRE1}=0.\)

  • Imposed movements, of symmetry, on the faces of the cube belonging to the planes

\(X=-0.5\) \(\mathrm{DX}=0\)

\(Y=-0.5\) \(\mathrm{DY}=0\)

\(Z=-0.5\) \(\mathrm{DZ}=0\)

Loading

• • We progressively apply \(p={2.10}^{6}\mathrm{Pa}\) compression to the faces of the cube belonging to the planes: \(X=0.5\), \(Y=0.5\) and \(Z=0.5\)

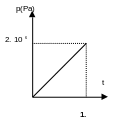
• • • Step B: \(t\in \text{]}\mathrm{1,2}\mathrm{.}\text{]}\)

From the state of constraints obtained at instant \(t=1.s\), the following conditions are applied to the faces of the cube:

Movations

• • For the face belonging to plane \(Z=0.5\), the \(\mathrm{DZ}\) displacement is gradually applied, following a ramp:

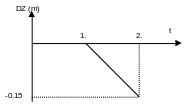
• • For faces belonging to planes \(X=-0.5,Y=-0.5,Z=-0.5\), symmetry conditions are applied.

Loads: the loads applied are constant:

• • • • Face belonging to plane \(X=0.5\) \(p={2.10}^{6}\mathrm{Pa}\)

      • Face belonging to plane \(Z=0.5\) \(p={2.10}^{6}\mathrm{Pa}\)