2. Benchmark solution#

2.1. Elastic solution without shrinkage#

We place ourselves under the following hypotheses:

  • the sections of the beams remain flat

  • there is perfect adhesion between concrete and steel

  • the behavior is linear elastic

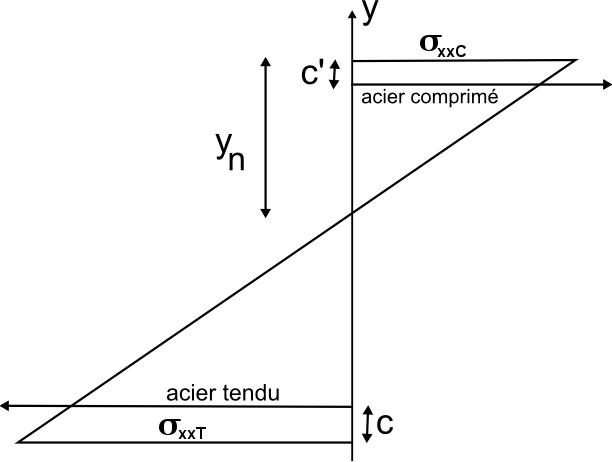
_images/1000000000000264000001CE80751FB5BF3E6AD8.png

We can therefore evaluate the position of the neutral axis of the beam \({y}_{n}\) according to the position of the steels. To do this, the following equation must be solved:

(2.1)#\[{y}_{n}\left(2\frac{n}{b}\left({A}_{s}+{A}_{S}\text{'}\right)+2h\right)-\left(2\frac{n}{b}\left({A}_{S}\text{'}c\text{'}+{A}_{s}\left(h-c\right)\right)+{h}^{2}\right)=0\]

With:

\({A}_{s}\) and \({A}_{s}\text{'}\): steel surfaces respectively stretched and compressed in the section

\(c\text{'}\) and \(c\text{'}\): concrete coating respectively below the stretched steels and above the compressed steels

\(b\) and \(h\): respectively the width and the height of the beam section

\(n\mathrm{=}\frac{{E}_{a}}{{E}_{b}}\): ratio between the Young’s modulus of concrete and steel

The longitudinal compression stress \({\mathrm{\sigma }}_{\mathit{xxC}}\) as a function of the bending moment and the position of the neutral axis.

(2.2)#\[{\mathrm{\sigma }}_{\mathit{xxC}}=\frac{\mathit{Mf}}{\left({A}_{s}n\frac{{\left(h-c-{y}_{n}\right)}^{2}}{{y}_{n}}+{A}_{s}\text{'}n\frac{{\left({y}_{n}-c\text{'}\right)}^{2}}{{y}_{n}}+\frac{{\mathit{by}}_{n}^{2}}{3}+b\frac{{\left(h-{y}_{n}\right)}^{3}}{{y}_{n}}\right)}\]
(2.3)#\[\mathit{Mf}(x)=\frac{\mathit{Fx}}{2}\]

The digital application gives:

(2.4)#\[{y}_{n}=0.2674\]

And in \(x\mathrm{=}2.5m\) and \(y\mathrm{=}\mathrm{0,25}m\), the maximum compressive stress is equal to:

(2.5)#\[{\mathrm{\sigma }}_{\mathit{xxC}}=-2.05\mathit{MPa}\]

Using the linearity of the stresses in the section, the maximum tensile stress is

(2.6)#\[{\mathrm{\sigma }}_{\mathit{xxT}}=1.78\mathit{MPa}\]

2.2. Solution with withdrawals#

Deformations due to desiccation shrinkage and thermal expansion can easily be evaluated where the values of water concentration and temperature are known. For endogenous withdrawal, the degree of hydration is evaluated from the interpolation used to define the hydration parameters. We have:

  • in \(G\) to \(t>30j\):

\(T=20°C\) so \({\mathrm{\epsilon }}_{\mathit{th}}=\mathrm{\alpha }(T-{T}_{\mathit{ref}})=0\)

\(C\mathrm{=}50l\mathrm{/}{m}^{3}\) so \({\mathrm{\epsilon }}_{\mathit{sec}}=-{K}_{\mathit{des}}({C}_{0}-C)=-5.6e-4\)

\(\mathrm{\xi }=\mathrm{0,95}\) so \({\mathrm{\epsilon }}_{\mathit{endo}}=-{B}_{\mathit{endo}}\mathrm{\xi }=-\mathrm{8,55e-5}\)

  • in \(G\) to \(t>30j\):

\(T=40°C\) so \({\mathrm{\epsilon }}_{\mathit{th}}=\mathrm{\alpha }(T-{T}_{\mathit{ref}})=2.4e-5\)

\(C\mathrm{=}70l\mathrm{/}{m}^{3}\) so \({\mathrm{\epsilon }}_{\mathit{sec}}=-{K}_{\mathit{des}}({C}_{0}-C)=-4e-4\)

\(\mathrm{\xi }=\mathrm{0,95}\) so \({\mathrm{\epsilon }}_{\mathit{endo}}=-{B}_{\mathit{endo}}\mathrm{\xi }=-\mathrm{8,55e-5}\)

The constraints in \(G\) are not calculated analytically but result from a calculation on a very fine mesh (32000 HEXA20 and 155369 nodes).