1. Reference problem#
1.1. Geometry#
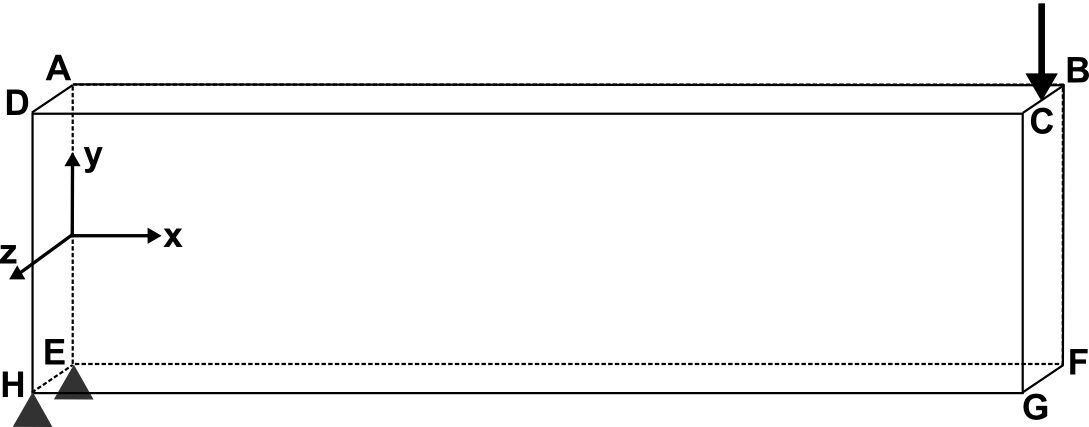
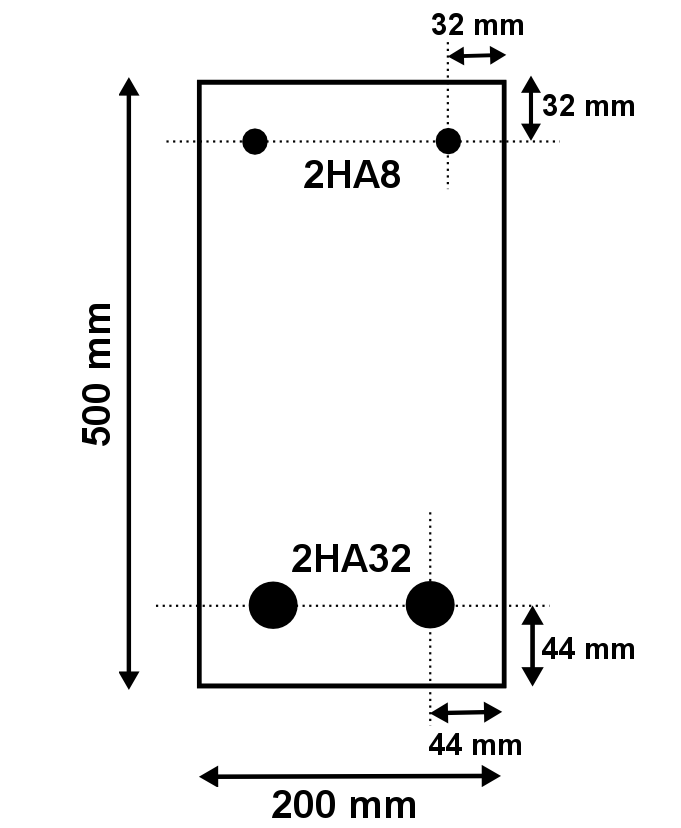
It is a \(5m\) long reinforced beam of which only a quarter can be modelled thanks to the symmetries. The dimensions are given in millimeters.
|
1.2. Initial condition and thermal loads#
The initial temperature is uniform at \(20°C\). Concrete is subject to thermo-hydration.
The temperature is set to \(20°C\) on the face \(\mathrm{EFGH}\) noted HAUT in the mesh.
The temperature is constant at \(20°C\) for up to 10 days then varies linearly from \(20\mathrm{°}\mathrm{C}\) to \(40\mathrm{°}\mathrm{C}\) between 10 days and 30 days and is then constant at \(40\mathrm{°}\mathrm{C}\) on the \(\mathrm{ABCD}\) side marked BAS in the mesh.
1.3. Initial condition and drying loads#
The initial water concentration is uniform at \(120l\mathrm{/}{m}^{3}\).
The water concentration is set to \(50l\mathrm{/}{m}^{3}\) on the \(\mathrm{EFGH}\) side marked HAUT.
The water concentration is set to \(70l\mathrm{/}{m}^{3}\) on the \(\mathrm{ABCD}\) side.
1.4. Boundary conditions and mechanical loads#
Symmetry conditions
The plate is stuck next \(\mathrm{Ox}\) on the side \(\mathrm{BCGF}\) noted SYME_X and next \(\mathrm{Oz}\) on the side \(\mathrm{ABFE}\) noted SYME_Z.
Boundary condition
The plate is stuck next \(\mathrm{Oy}\) on the side \(\mathrm{HE}\) noted APPUI.
Loading
It is subjected to a force \(\frac{F}{4}=3840N\) following \(\mathrm{Oy}\) distributed on the side \(\mathrm{BC}\), denoted by FORCE, which is equivalent to a total force of \(F=15360N\) on the entire beam. The force is applied at the final moment of each calculation (in modeling A to the only time step taken and in modeling B to \(t\mathrm{=}100\mathit{jours}\)).
1.5. Thermal properties of materials#
The characteristics of concrete are:
Heat capacity \(\mathrm{\rho }{C}_{p}=2.4{e}^{6}J/{m}^{3}/°C\);
Conductivity \(\mathrm{\lambda }=1W/m/°C\);
and the following characteristics relating to moisturizing behavior:
heat per degree of hydration: \({Q}_{0}\mathrm{=}{1.14e}^{8}J\mathrm{/}{m}^{3}\)
affinity as a function of hydration (polynomial evaluation of the known function by points) and of temperature (table):
\(A(\mathrm{\xi },T)=(50.12{\mathrm{\xi }}^{6}-190.76{\mathrm{\xi }}^{5}+258.38{\mathrm{\xi }}^{4}-123.71{\mathrm{\xi }}^{3}-11.82{\mathrm{\xi }}^{2}+15.37\mathrm{\xi }+2.43)\mathrm{exp}(\frac{-{\mathit{QSR}}_{K}}{(273.15+T)})\)
with Arrhenius constant: \({\mathit{QSR}}_{K}=4000K\).
Note: The Arrhenius constant is always expressed in degrees Kelvin. Temperatures are expressed in \(°C\).
1.6. Properties of drying materials#
We use the law of diffusion SECH_GRANGER:
\(D(C,T)=A\cdot \mathrm{exp}(\mathit{BC})\frac{T}{{T}_{0}}\mathrm{exp}\left[-\frac{{Q}_{s}}{R}\left(\frac{1}{T}-\frac{1}{{T}_{0}}\right)\right]\)
\(A=3.3e-13{m}^{2}/s\);
\(B=0.05\);
\(\mathit{QSR}=4000K\)
\({T}_{0}=293°K=20°C\)
1.7. Mechanical properties of materials#
The behavior is elastic.
The characteristics of steels are:
Young’s module \({E}_{a}=200000\mathrm{MPa}\);
Poisson’s ratio \(\mathrm{\nu }=0.3\);
The characteristics of concrete are:
Young’s module \({E}_{b}=32000\mathit{MPa}\) for modeling A. In modeling B, it varies linearly as a function of temperature from \({E}_{b}=30000\mathrm{MPa}\) for \(T=0°C\) to \({E}_{b}\mathrm{=}40000\mathit{MPa}\) for \(T=100°C\);
Poisson’s ratio \(\mathrm{\nu }=0.2\);
Thermal expansion \(\mathrm{\alpha }=1.2e-6\) at the reference temperature of \({T}_{\mathrm{ref}}=20°C\)
Desiccation shrinkage coefficient \({K}_{\mathit{des}}\mathrm{=}8e-6\)
Endogenous shrinkage coefficient \({B}_{\mathit{endo}}\mathrm{=}9e-5\)