6. D modeling#
6.1. Characteristics of modeling#
The symmetry of the problem makes it possible to represent only a quarter of the model in 3D: The sphere and the block are represented respectively by a quarter sphere and a quarter of a cylinder, meshed with 3D solid elements CUB8.
A node-mesh contact is defined between the sphere and the block.
An imposed displacement load is applied to the upper part of the sphere, which is rigidified by a high Young’s modulus.
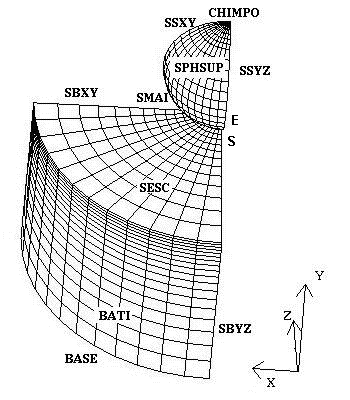
Boundary condition:
|
the nodes located in plane \((O,y,z)\) (node groups \(«\mathrm{SBYZ}»\) and \(«\mathrm{SSYZ}»\)) are blocked in the direction \(X\) (DX= 0), |
the nodes located in plane \((O,x,y)\) (node groups \(«\mathrm{SBXY}»\) and \(«\mathrm{SSXY}»\)) are blocked in the direction \(Z\) (DZ= 0). |
|
|
the nodes of \(«\mathrm{BASE}»\) (plane \(Y=0.\)) are blocked in the directions \(X\), \(Y\), and \(Z\) (DX = DY = DZ = 0). |
Rigid body movements are suppressed by imposing a following link y between node \(E\) belonging to the sphere and node \(S\) belonging to the massif.
Loads:
An imposed displacement is applied to the upper part of the sphere (group of nodes \(«\mathrm{CHIMPO}»\)) in the direction \(Y\): Loading from 0 to \(–100.\mathrm{mm}\)
6.2. Characteristics of the mesh#
Number of knots: 6993
Number of meshes and type: 5544 HEXA8, 407 PENTA6 and 191 QUAD4
6.3. Tested values#
Identification |
Movations |
Reference |
Aster |
% tolerance |
Reaction \((N)\) |
|
—3.201351E+06 |
-3.82828724E+06 |
25 |
Reaction \((N)\) |
|
—6.402702E+06 |
-7.38942843E+06 |
20 |
Reaction \((N)\) |
|
—9.604053E+06 |
-1.06420713E+07 |
15 |
Reaction \((N)\) |
|
—1.280540E+07 |
-1.28912992E+07 |
10 |
Reaction \((N)\) |
|
—1.600675E+07 |
-1.56376456E+07 |
5 |
6.4. notes#
The results are almost identical to those of modeling C. But the calculation is even more tedious because a quarter of the sphere is meshed.