3. Modeling A#
3.1. Characteristics of modeling#
The symmetry of revolution of the problem allows axisymmetric modeling: The sphere and the block are represented respectively by a half disk and the section of half of the block, meshed with axisymmetric 2D elements.
A node-mesh contact is defined between the two structures.
An imposed displacement load is applied to the upper part of the sphere, which is rigidified by a high Young’s modulus.
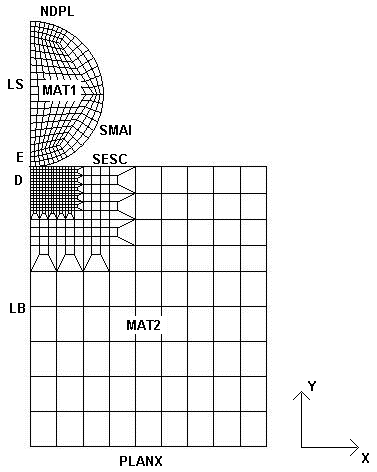
Boundary condition:
symmetry of revolution: the nodes located on the \(Y\) axis (group of nodes \(«\mathrm{LB}»\) and \(«\mathrm{LS}»\)) are blocked in the direction \(X\) (DX = 0),
embedding the base: the nodes in group \(«\mathrm{PLANX}»\) are blocked in the directions \(X\) and \(Y\) (DX = DY = 0),
rigid body movements are suppressed by imposing a link following \(y\) between node \(E\) belonging to the sphere and node \(D\) belonging to the massif.
Loads:
An imposed displacement is applied to the upper part of the sphere (group of nodes \(«\mathrm{NDPL}»\)) in the direction \(Y\): Loading from 0 to \(–100.\mathrm{mm}\)
3.2. Characteristics of the mesh#
Number of knots: 916
Number of meshes and type: 625 QUAD4 and 289 SEG2
3.3. Tested values#
Identification |
Movement \((\mathrm{mm})\) |
Reference |
Aster |
% tolerance |
Reaction \((N)\) |
20 |
—2.03804E+06 |
—2.06806E+06 |
5 |
Reaction \((N)\) |
40 |
—4.07608E+06 |
—4.04698E+06 |
5 |
Reaction \((N)\) |
60 |
—6.11412E+06 |
—5.82730E+06 |
5 |
Reaction \((N)\) |
80 |
—8.15217E+06 |
—7.66632E+06 |
10 |
Reaction \((N)\) |
100 |
—1.01902E+07 |
—9.11899E+06 |
15 |
3.4. notes#
The most important error is for the last result. Nevertheless, it is still acceptable.
We illustrated the deformation of the massif at the final time step:
