1. Reference problem#
1.1. Geometry and meshing#
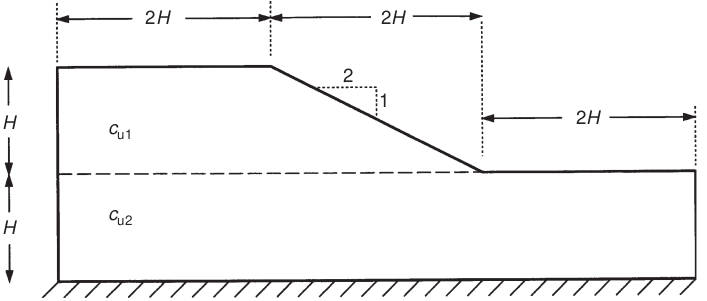
We study the stability of a clay slope on a weak foundation,
whose geometry is shown in fig1-geom-ssnp507.
The geometric parameter H is fixed at 3 m in this test case,
which has no influence on the stability result since the cohesion of the clay
is assumed to be correlated with the size of the slope.
1.2. Material properties#
Table 1: Property of slope materials
Foundation |
Slope |
|
Density \(\rho\) (kg/m³) |
3000 |
|
Young’s Module \(E\) (MPa) |
100 |
|
Poisson’s Ratio \(\nu\) |
0.3 |
|
Cohesion force \(c\) (kPa) |
\(0.25\lambda\rho gH\) |
|
Expansion angle \(\psi\) (deg) |
0 |
|
Friction angle \(\varphi\) (deg) |
0 |
The mechanical properties of the materials in the model are presented in the Tableau 1.
In order to simulate the undrained behavior of clay, the angles of friction and expansion are rubbish. So we find the Tresca criterion describing the resistance of the soil to shear. The weakness of the foundation is described by parameter \(\lambda\) defined as the relationship between the cohesions of the foundation and the slope:
\(\lambda =\dfrac{{c}_{u2}}{{c}_{u1}}\)
1.3. Boundary conditions and loads#
The boundary conditions applied to the model are as follows:
Bottom of the embedded foundation (DX=0, DY=0), and the vertical sides normally locked (DX=0).
The following mechanical loads are applied to the model:
Gravity with \(g=\mathrm{9,81}m/{s}^{2}\)