3. Modeling A#
3.1. Characteristics of modeling#
In this modeling, the extended finite element method (\(\text{X-FEM}\)) is used. Finite elements are linear.
We define a radius of enrichment of elements X- FEM crack bottom \({R}_{\mathit{ENRI}}=0.5\). This enrichment radius makes it possible to more accurately capture the singular asymptotic solution at the bottom of the crack. The relatively large radius size (25% of the crack length) does not introduce conditioning problems, taking into account the new approximation at the bottom of the crack [R7.02.12].
3.2. Characteristics of the mesh#
The mesh at the center of the test piece is refined in order to optimize the calculation of the solution moving in the vicinity of the crack [].
NOMBRE OF NOEUDS 4088
NOMBRE OF MAILLES 4360
SEG2 80
TRIA3 466
QUAD4 3814
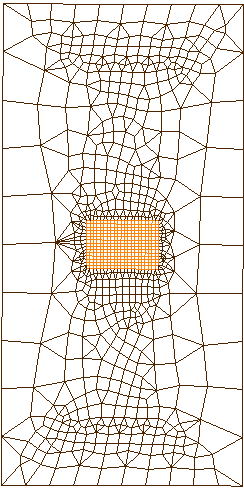
Figure 3.2-1: Domain mesh
3.3. Tested sizes and results#
On the background of the crack in opening \(P2=(a\mathrm{,0})\), the stress intensity factor \({K}_{I}\) given by the command CALC_G is tested, compared to the analytical value explained in paragraph [5].
For method \(G-\mathit{thêta}\) (command CALC_G), the following crowns of the theta field are chosen:
Crown 1 |
Crown 2 |
Crown 3 |
Crown 3 |
Crown 4 |
Crown 5 |
Crown 6 |
|
Rinf |
0.1 |
0.2 |
0.2 |
0.3 |
0.3 |
0.1 |
0.2 |
Rsup |
0.2 |
0.3 |
0.3 |
0.3 |
0.4 |
0.4 |
0.4 |
Identification |
Reference type |
Reference value |
Precision |
CALC_G /K1 |
“ANALYTIQUE” |
0.88629 |
|
CALC_G /K2 |
“ANALYTIQUE” |
0.00 |
|
CALC_G /G |
“ANALYTIQUE” |
7.85514E-07 |
|
3.4. Additional results#
Here is the displacement field calculated by Aster, without activating the crack lip contact algorithm:
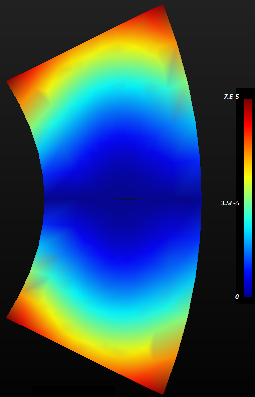
Figure 3.4-1: Field of movement (with offset)