1. Reference problem#

1.1. Geometry#

Consider the geometry described in the figure where the dimensions in mm are as follows:

\({d}_{1}=0.2{d}_{2}=1.2{d}_{3}=10.6r=0.75{h}_{1}=0.95{h}_{2}=4{a}_{1}=0.3{a}_{2}=0.2\)

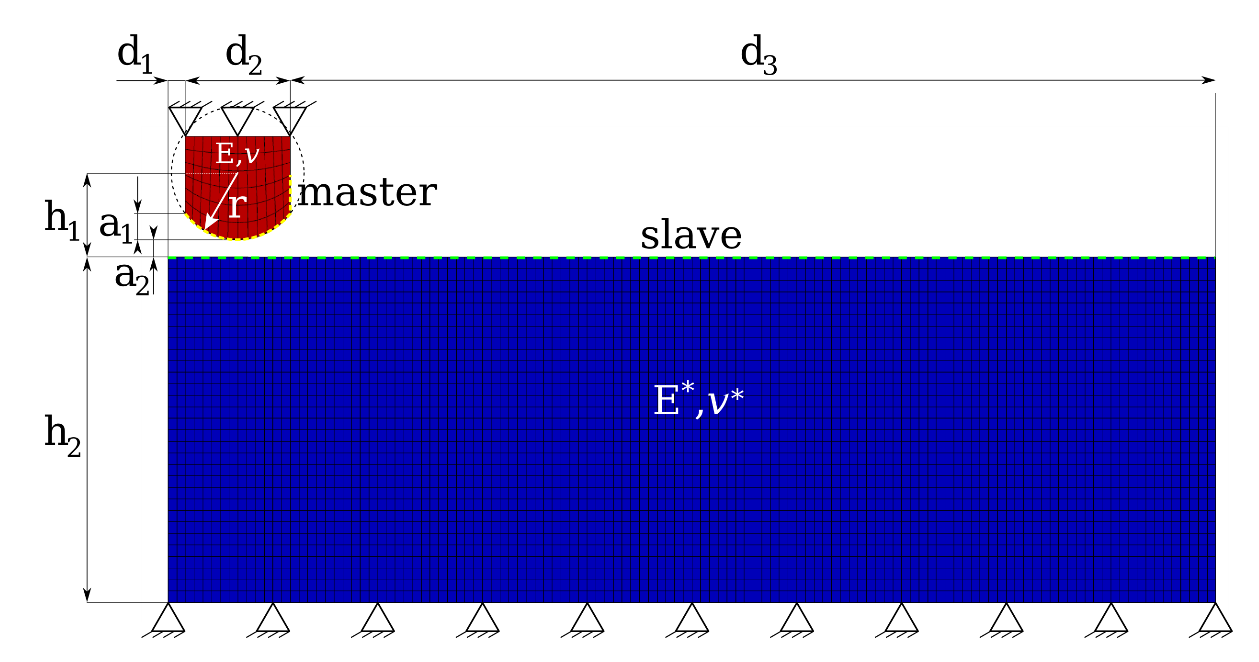
Figure 1: Problem geometry (image from [1])

The 2 materials are isotropic elastic whose properties are:

:math:`Etext{}=6.896E8mathrm{MPa}` \(\nu \text{*}=0.32\)

They are both represented in large deformations according to the model of Simo and Miehe.

The lower edge of the massif is embedded.

The upper edge of the stamp is subjected to an imposed displacement given by:

\(\begin{array}{ccc}t\in [\mathrm{0,1}]& {u}_{x}=0& {u}_{y}=t\\ t\in [\mathrm{1,2}]& {u}_{x}=10(t-1)& {u}_{y}=1\end{array}\)

For contact, the punch is master and the massive slave. We consider Coulomb friction with a coefficient \(\mu =0.3\).

Néant