1. Reference problem#

1.1. Geometry#

In the Cartesian coordinate system \((x,y)\), consider an elastic rectangular flat plate denoted by \(\Omega =]\mathrm{0,}L[\times ]\mathrm{0,}H[\) (see [Figure 1.1-a]). Note \({\Gamma }_{0}\mathrm{=}\left\{0\right\}\mathrm{\times }\mathrm{]}\mathrm{0,}H\mathrm{[}\) the left side of the domain and \(\mathrm{\partial }\Omega \mathrm{\setminus }{\Gamma }_{0}\) the complementary part of the edge.

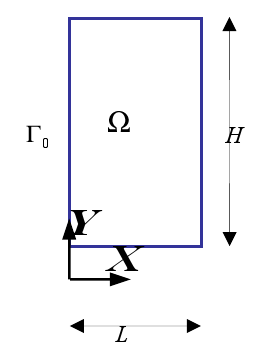
_images/1000000000000114000001621B239BC3370174F8.png

Figure 1.1-a .1-a: Plate scheme

Domain \(\Omega\) dimensions:

\(L=\mathrm{1mm},H=2\pi \text{mm}\)

1.2. Material properties#

The material is elastic with a critical stress and a tenacity chosen arbitrarily:

\(E=10\text{MPa},\nu =\mathrm{0,}{\sigma }_{c}=1.1\text{MPa},{G}_{c}=0.9{\text{N.mm}}^{-1}\)

1.3. Boundary conditions and loads#

The boundary conditions are determined by the analytical solution presented in the next part in such a way that they lead to a crack with a non-constant jump along \({\Gamma }_{0}\). The loading corresponds to a displacement imposed on the edges of the plate: (see [Figure1.3-a]).

\(u=U(x,y)\)

on \(\Omega /{\Gamma }_{0}\)

\(u={U}_{0}\delta (y)-(y)\)

on \({\Gamma }_{0}\)
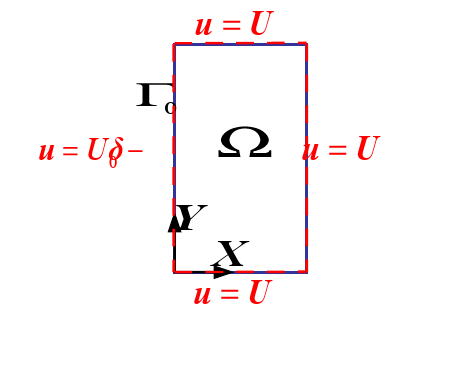
_images/10000000000001C60000016FA6F563CD4C6800DD.png

Figure 1.3-a: Load Diagram

The values \(U,{U}_{0}\) and \(\delta\) are set when constructing the reference solution in the next part.