1. Reference problem#
1.1. Geometry#
We consider an arc \(\mathit{AB}\) with radius \(100\mathit{cm}\), center \(C\) and aperture \(45°\)
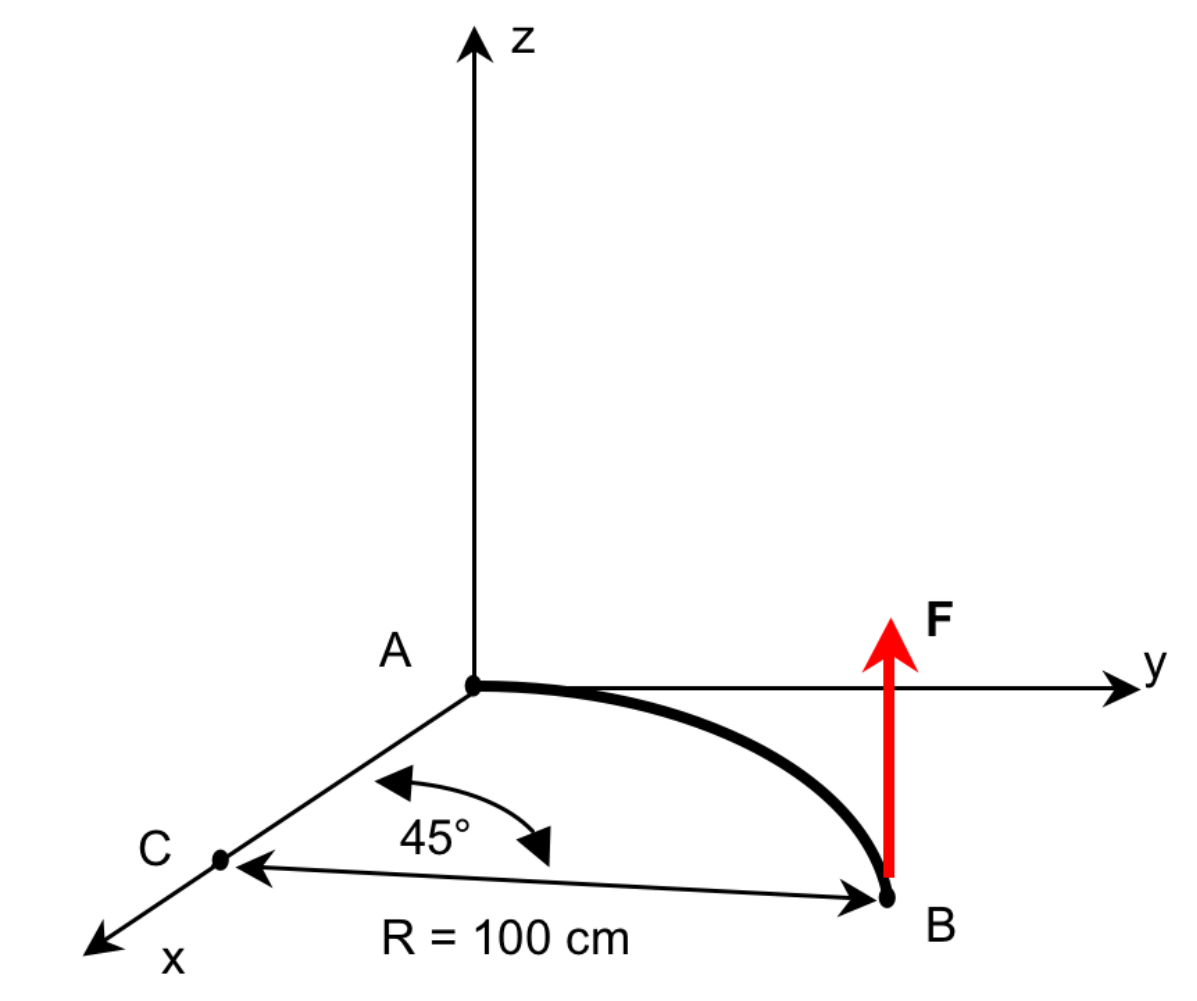
Illustration 1.1.1: arc geometry
Coordinates of the points (in \(\mathit{cm}\)):
\(A\) |
|
|
|
\(x\) |
0 |
29.3 |
100 |
\(y\) |
0 |
70.7 |
0 |
\(z\) |
0 |
0 |
0 |
1.2. Characteristics of the section#
The arc has a square cross section of \(1\mathit{cm}\) by \(1\mathit{cm}\).
\(A\mathrm{=}1{\mathit{cm}}^{2}\) |
\({I}_{y}\mathrm{=}{I}_{z}\mathrm{=}0.0833{\mathit{cm}}^{4}\) |
\({A}_{y}\mathrm{=}{A}_{z}\mathrm{=}1.2\) |
1.3. Material properties#
\(E\mathrm{=}1\mathit{MPa}\) |
\(\nu \mathrm{=}0.0\) |
1.4. Boundary conditions and loading#
Boundary conditions are imposed at point \(A\) (arc embedment): \(\mathit{DX}\mathrm{=}\mathit{DY}\mathrm{=}\mathit{DZ}\mathrm{=}\mathit{DRX}\mathrm{=}\mathit{DRY}\mathrm{=}\mathit{DRZ}\mathrm{=}0\) |
|
At the free end at point \(B\), a vertical loading (perpendicular to the plane of the arc) is imposed at the free end at point: \(\mathrm{600N}\) \(\mathit{FZ}\mathrm{=}\text{600}\mathrm{\times }t\) |