3. Modeling A#
3.1. Characteristics of modeling#
Concrete is modelled with the Mazars damage law in version \(1D\) (Mazars_GC) [R7.01.08]. The material parameters used are as follows:
\(\mathit{AC}=1.71202987\) \(\mathit{BC}=2.01163780E+03\) \(\mathit{BT}=1.21892353E+04\) \(\mathit{BETA}=1.10E+00\)
\(\mathit{AT}=1.0E+00\) \(\mathit{EPSD}0=8.20396008E-05\)
3.2. Tested sizes and results#
The arrow is that of the center of the beam, the local results (stresses, deformations) are those of the second Gauss point of the 9th element (the closest to the middle of the beam).
Supportive reaction to point \(A\):
Arrow (m) |
Height |
Location |
Reference type |
Tolerance |
||
1.00E-03 |
|
DY |
DY |
Group:A |
NON_REGRESSION |
3.0E-04 |
1.40E-02 |
|
DY |
DY |
Group:A |
NON_REGRESSION |
3.0E-04 |
2.68E-02 |
|
DY |
DY |
Group:A |
NON_REGRESSION |
3.0E-04 |
Stress in tensile steels:
Arrow (m) |
Height |
Location |
Reference type |
Tolerance |
1.00E-03 |
|
Size:M9, stitch:2 subpoint:41 |
NON_REGRESSION |
3.0E-04 |
1.40E-02 |
|
Size:M9, stitch: 2 subpoint:41 |
NON_REGRESSION |
3.0E-04 |
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:41 |
NON_REGRESSION |
0.0E+00 |
Stress in compressed steels:
Arrow (m) |
Height |
Location |
Reference type |
Tolerance |
1.00E-03 |
|
Size:M9, stitch:2 subpoint:44 |
NON_REGRESSION |
3.0E-04 |
1.40E-02 |
|
Size:M9, stitch: 2 subpoint:44 |
NON_REGRESSION |
3.0E-04 |
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:44 |
NON_REGRESSION |
3.0E-04 |
Deformation in tensile steels:
Arrow (m) |
Height |
Location |
Reference type |
Tolerance |
1.00E-03 |
|
Size:M9, stitch:2 subpoint:41 |
NON_REGRESSION |
3.0E-04 |
1.40E-02 |
|
Size:M9, stitch: 2 subpoint:41 |
NON_REGRESSION |
3.0E-04 |
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:41 |
NON_REGRESSION |
3.0E-04 |
Stress in compressed concrete:
Arrow (m) |
Height |
Location |
Reference type |
Tolerance |
1.00E-03 |
|
Size:M9, stitch:2 subpoint:1 |
NON_REGRESSION |
3.0E-04 |
1.40E-02 |
|
Size:M9, stitch: 2 subpoint:1 |
NON_REGRESSION |
3.0E-04 |
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:1 |
NON_REGRESSION |
3.0E-04 |
Stress in stretch concrete:
Arrow (m) |
Height |
Location |
Reference type |
Tolerance |
1.00E-03 |
|
Size:M9, stitch:2 subpoint:40 |
NON_REGRESSION |
3.0E-04 |
1.40E-02 |
|
Size:M9, stitch: 2 subpoint:40 |
NON_REGRESSION |
3.0E-04 |
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:40 |
NON_REGRESSION |
3.0E-04 |
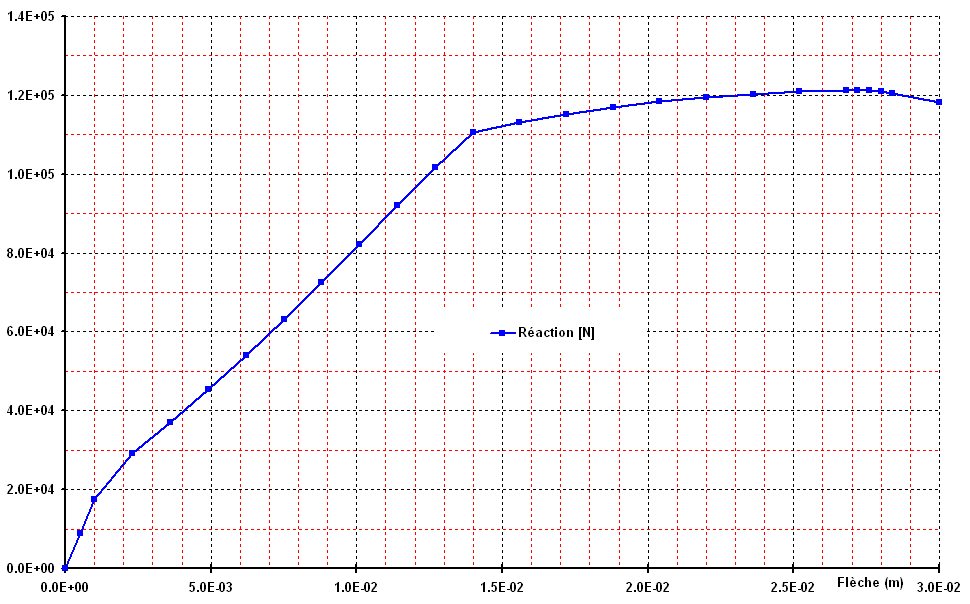
Figure 3.2-a: reaction on a support, depending on the arrow in the center. **
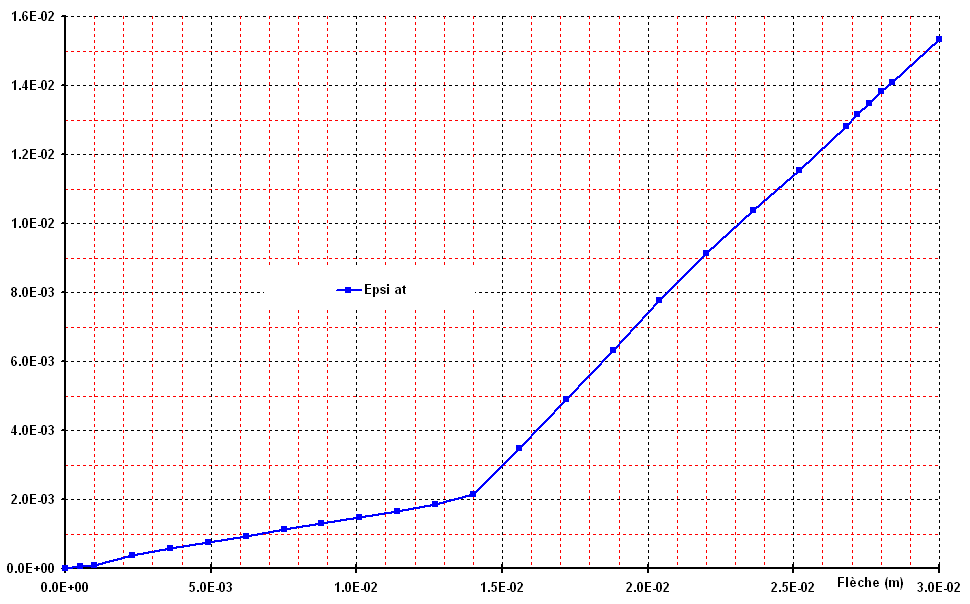
Figure 3.2-b: d deformation of tensile steels, as a function of the arrow in the center.
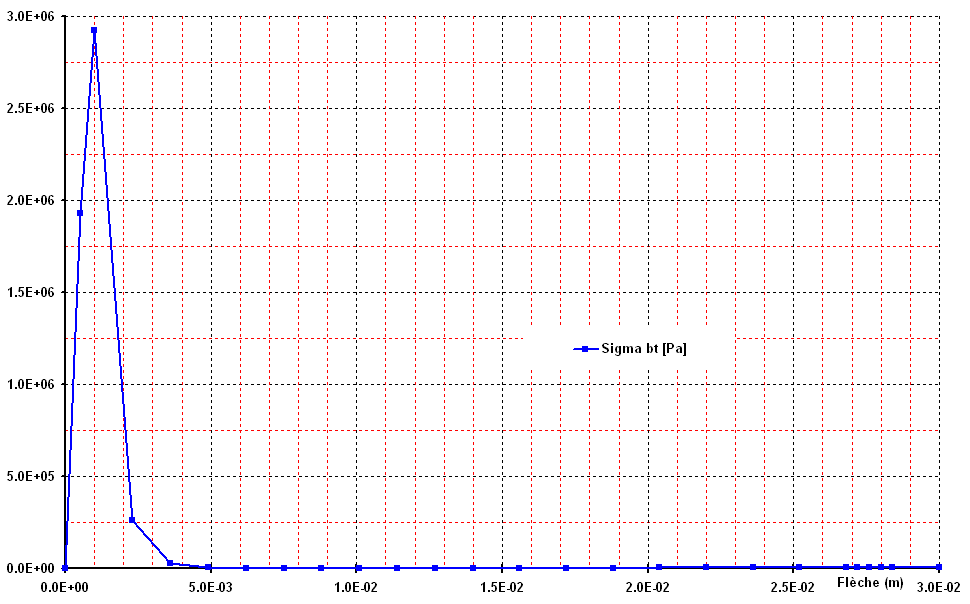
Figure 3.2-c: tension concrete stress, depending on the arrow in the center. **
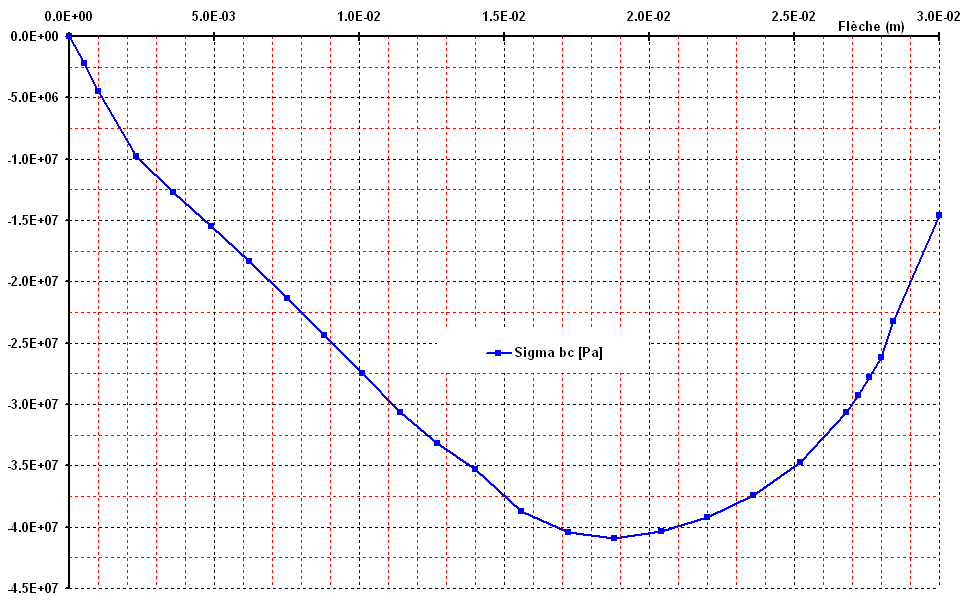
Figure 3.2-d: C**stresses compressed concrete, depending on the arrow in the center.**
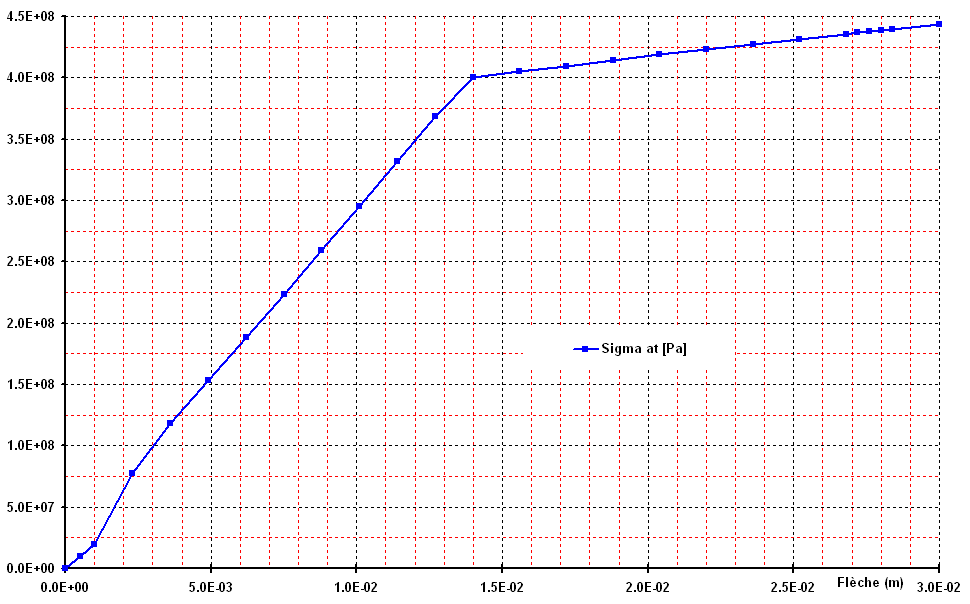
Figure 3.2-e : tensile steel stress, depending on the arrow in the center.
We also validate the calculation of option EPSP_ELGA (plastic deformation) for elements POU_D_EM. To do this, we take advantage of the fact that the equivalent plastic deformation is the first internal variable of law VMIS_ISOT_TRAC, so this provides a reference value.
Arrow (m) |
Height |
Location |
Reference Value |
Reference Type |
Tolerance |
|
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:44 |
NON_REGRESSION |
|||
2.68E-02 |
|
Size:M9, stitch: 2 subpoint:44 |
-5.6713030306951E-04 |
|
3.0E-04 |
3.0E-04 |
3.3. notes#
There is no particular refinement of the time steps to be taken. There are 26 time steps (triggering a subdivision for non-convergence in 10 iterations), which corresponds to 110 Newton iterations for the complete calculation.
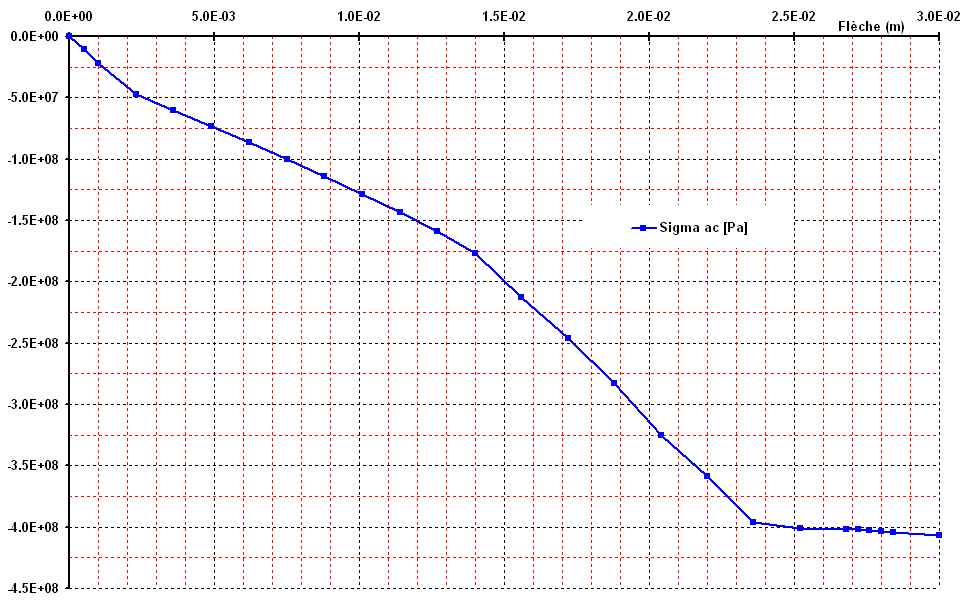
Figure 3.3-a: c stresses compressed steel, depending on the arrow in the center.
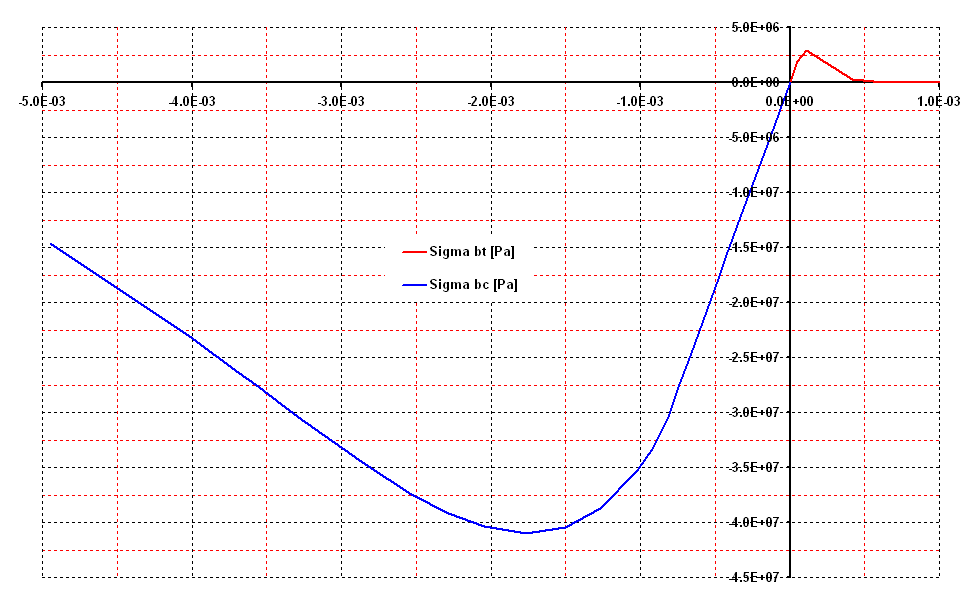
Figure3.3-b: concrete behavior.