1. Description

1.1. Geometry

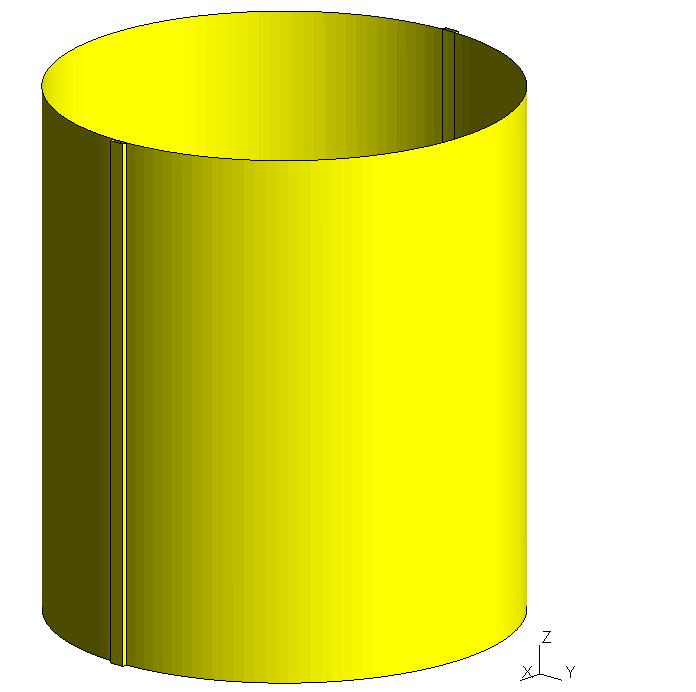
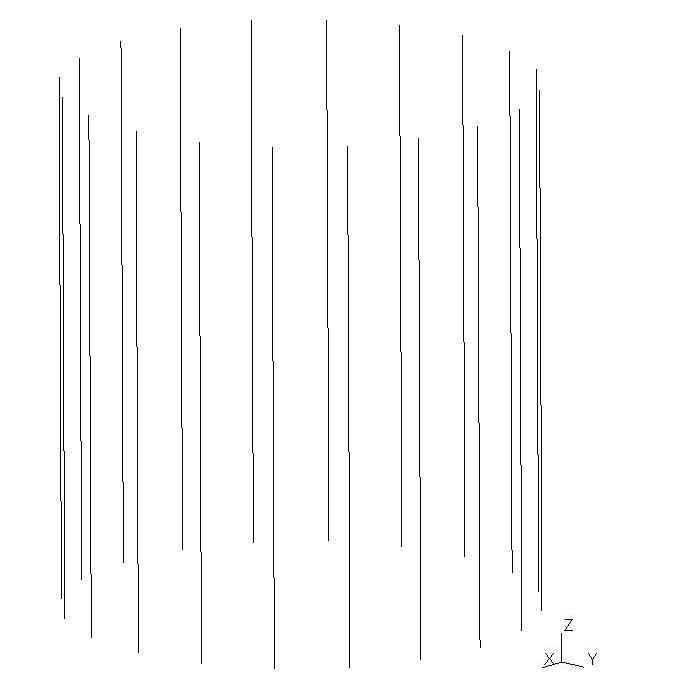
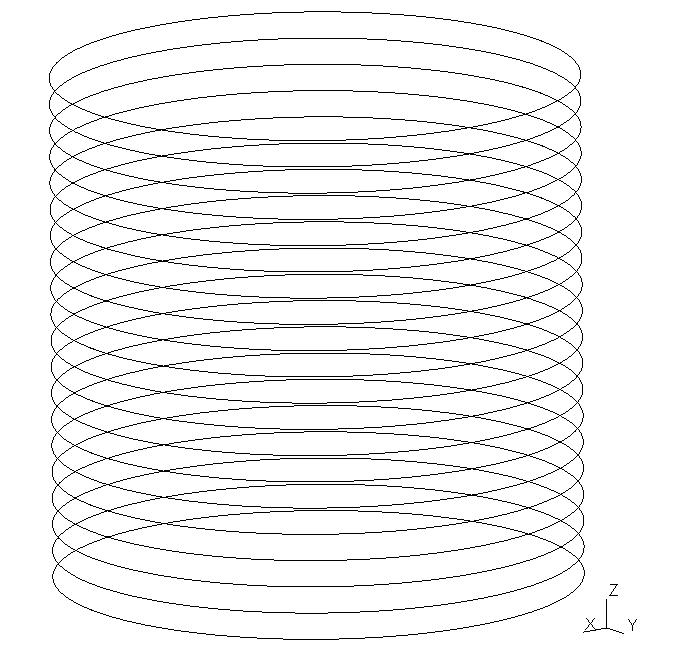
The study model is a cylindrical envelope with an average radius \(R=21.9m\), a height \(H=49.6m\) and a thickness \(t=0.6m\). The cable anchors on the sides of the cylinder have a length of \(L=1.5m\) and a width of \(l=0.5m\). As for the cables, they are positioned on the outer skin of the cylinder. They are then offset by a distance \(e=0.25m\). The model is composed of \(20\) horizontal cables and \(20\) vertical cables. The figures below show the various components of the study model.

Cylinder	Vertical cables
Horizontal cables	Study model

1.2. Meshing

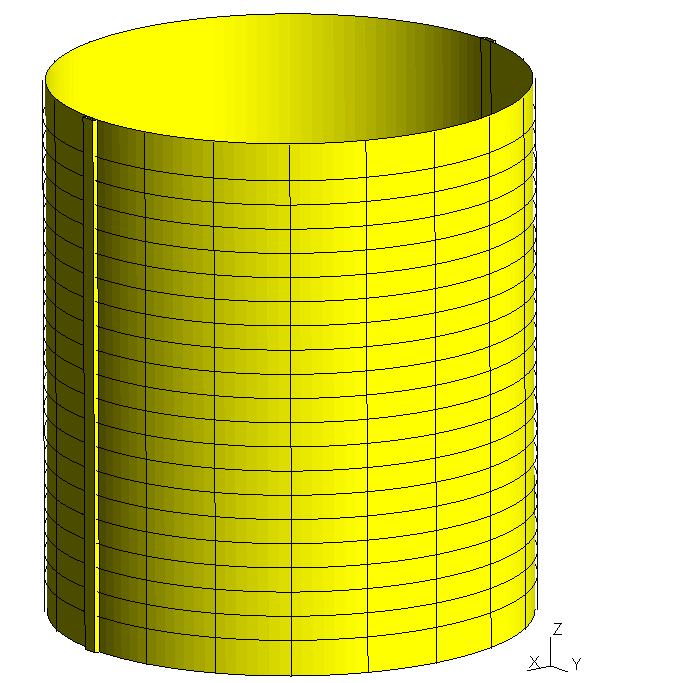
The cables are meshed with SEG2 meshes. The cylinder and the cable anchors are meshed with QUAD4 meshes. The discretization in space for the various components is at most \(f=1.0m\). The following figures represent the meshes for the various parts of the model.

Horizontal cable meshing	Vertical cable meshing
Cylinder mesh and anchors

1.3. Material properties

The properties of concrete for the cylinder and the anchors and of steel for the pretension cables are listed in the following table.

Material	Concrete	Steel
Young Module	\(4\times {10}^{10}\mathit{Pa}\)	\(1.93\times {10}^{11}\mathit{Pa}\)
Fish Coefficient	\(0.2\)	\(0.0\)
Density	\(2500\mathit{kg}/{m}^{3}\)	\(7850\mathit{kg}/{m}^{3}\)
Elastic limit stress	\(n/a\)	\(1.94\times {10}^{11}\mathit{Pa}\)

1.4. Boundary conditions and loads

The cylinder and the anchors are embedded at the top and bottom.

Initially, a voltage equal to \(3.75\times {10}^{6}N\) is imposed in the cables. The nodes at the ends of vertical and horizontal cables are considered « active. »

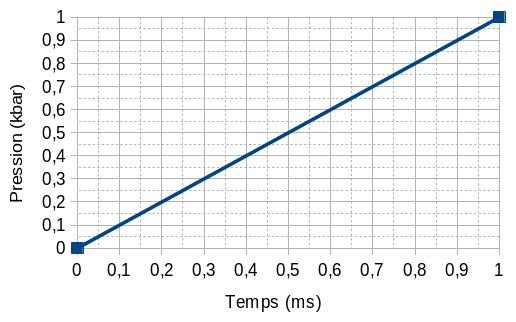
In a second step, the cylinder is subjected to an internal pressure that increases over time (from \({P}_{i}=0\mathit{Pa}\) to \({P}_{f}=1\mathit{kbar}\) in \(\Delta t\mathrm{=}1\mathit{ms}\)). This load is shown in the following graph.

1.5. Main stages of testing

Macro-control DEFI_CABLE_BP is used to obtain the kinematic relationships between the cylinder and the cables as well as the load related to the tension in the cables.

The macro-command CALC_PRECONT is then launched to prestress the structure using the tensions of the given cables.

The result of this prestress is given in initial state to the macro-command CALC_EUROPLEXUS in order to calculate the mechanical response of the prestressed cylinder to the internal pressure load.

To validate the results from CALC_EUROPLEXUS, we do the same calculation with the DYNA_NON_LINE operator.

From the two concept results obtained, the following are extracted:

• the evolution as a function of the time of movement on the reference point located halfway up the cylinder, i.e. in \((\mathrm{0,}R,H/2)\), noted \({N}_{\mathit{ref}}^{\mathit{cyl}}\).

• the resulting forces of membrane \(\mathit{Nxx}\) and \(\mathit{Nyy}\), at three different times in a cylinder cell having a node in common with the reference node of the cylinder, noted \({M}_{\mathit{ref}}^{\mathit{cyl}}\).

• the normal force in an element of the horizontal cable located closest to halfway up the cylinder and farthest from the anchors, noted \({\mathit{EL}}_{\mathit{ref}}^{\mathit{câb}}\).