1. Reference problem#
1.1. Geometry#
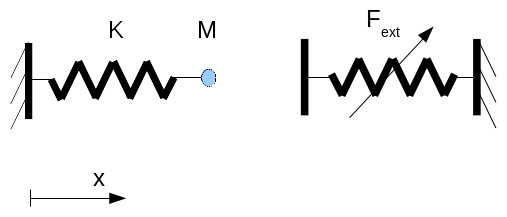
1.2. Material properties#
For models A and B
\(K={10}^{-7}N/m\)
\(M=1\mathrm{kg}\)
The reaction force \({F}_{\mathit{ext}}\) depends on the compression of the wall which follows the law below:
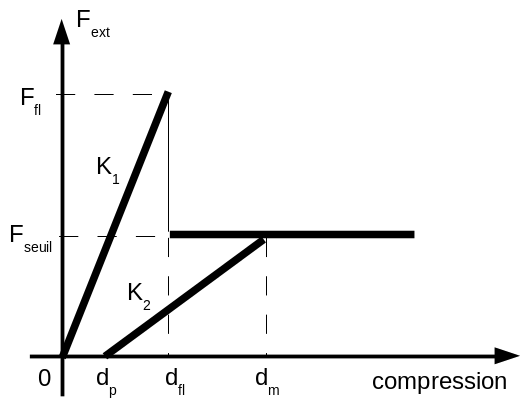
With:
\({K}_{1}=1N/m\)
\({F}_{\mathit{fl}}=1N\)
\({F}_{\mathit{seuil}}=0.5N\)
\({K}_{2}=0.5N/m\)
For C modeling
The force-compression relationship is shown in the figure below and in the details of the parameters.
With:
\({K}_{1}=1N/m\)
\({F}_{\mathit{fl}}=1N\)
\({F}_{\mathit{seuil}}=0.5N\)
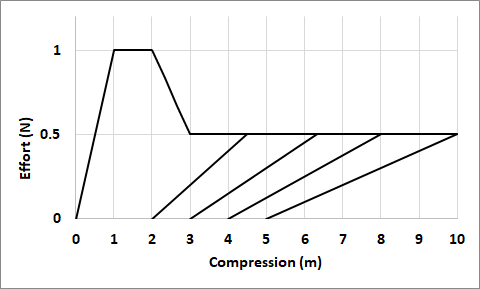
\(\text{LARG\_PLAT}=1m\)
\(\text{ENFO\_FL}=1m\)
\(\text{DEPL\_POST\_FL}=[\mathrm{2.,}\mathrm{3.,}\mathrm{4.,}5.]m\)
\(\text{RIGI\_POST\_FL}=[\mathrm{0.2,0}\mathrm{.15,0}\mathrm{.125,0}.1]N/m\)
For modelling D
The force-compression relationship corresponds to that used in the C modeling, but damping is added. Before buckling this damping is equal to \(\text{AMOR\_NOR}\), then it is divided by two during buckling.
\(\text{AMOR\_NOR}=10.N/m\mathrm{.}{s}^{-1}\)
\(\text{AMOR\_NOR}=5.N/m\mathrm{.}{s}^{-1}\)
\(\text{DEPL\_POST\_FL}=[\mathrm{5.,}\mathrm{5.,}\mathrm{5.,}5.]N/m\mathrm{.}{s}^{-1}\)
1.3. Boundary conditions and loads#
The movement of the mobile mass \(M\) along the \(x\) axis is imposed.
1.4. Initial conditions#
For models A and B
At the initial instant, the moving mass is just in contact against the wall (zero initial play) with an initial speed equal to \(2m/s\).
The wall has not yet undergone plastic deformation (wall not buckled).
For the*modelling*s*C and D
At the initial instant, the moving mass is just in contact against the wall (zero initial play) with an initial speed equal to \(2.828427125m/s\).
In the initial state, the wall has not yet undergone plastic deformation (wall not buckled).