1. Reference problem#

1.1. Geometry#

_images/Object_1.svg

The geometric dimensions chosen are as follows:

  • height

= \(0.5m\);

  • inner radius

= \(1m\);

  • outer radius

= \(1.2m\).

1.2. Material properties#

The cylinder is made of a homogeneous material that follows a linear elastic law of behavior:

  • \(E=10\mathrm{Pa}\);

  • \(\rho =1\mathrm{kg}/{m}^{3}\);

  • \(\nu =0.3\).

1.3. Boundary conditions and loads (Cf. [Figure 1.3-a])#

The volume force considered is radial, it varies quadratically with the radius: \({F}_{V}=\alpha \mathrm{.}{r}^{2}\) with \(\alpha =1N/{m}^{3}\).

The surface force in question is applied to the inner wall of the cylinder, perpendicular to the wall (equivalent to an internal pressure imposed on the cylinder): \({F}_{S}(r={R}_{\text{int}})=\mathrm{1N}/{m}^{2}\).

The boundary conditions make it possible to assume plane deformations on a section of the cylinder: vertical movements blocked on the upper and lower sections of the cylinder.

Note:

For 3D modeling, the suppression of natural modes is ensured by the 2D plane conditions applied to the lower section of the cylinder. This type of boundary conditions makes it possible to obtain an axisymmetric solution while moving, directly comparable with the analytical solution.

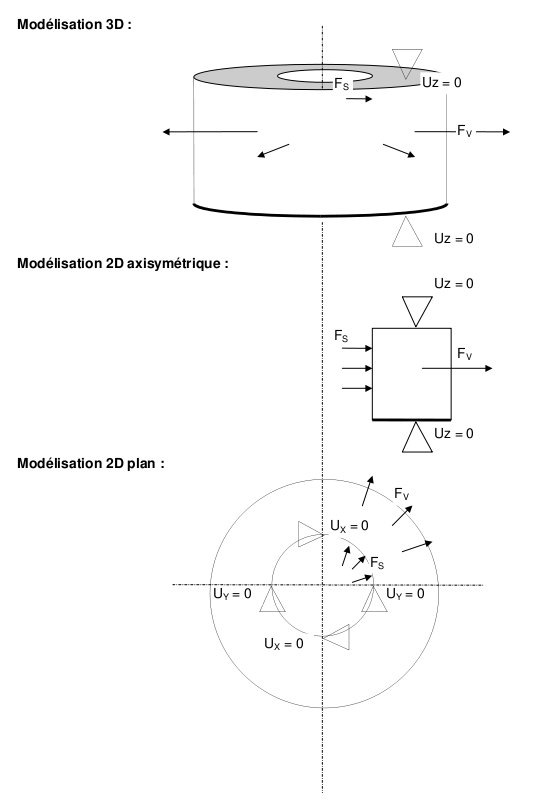
_images/100000000000022A000003256CD64CFF15EDD181.png

Figure 1.3-a: Boundary conditions and loads