5. C modeling#
5.1. Characteristics of C modeling#
z
3D, \(\mathrm{H20}\) and \(\mathrm{P15}\) meshes
y, v
F
B
y
x
A, E
B, F
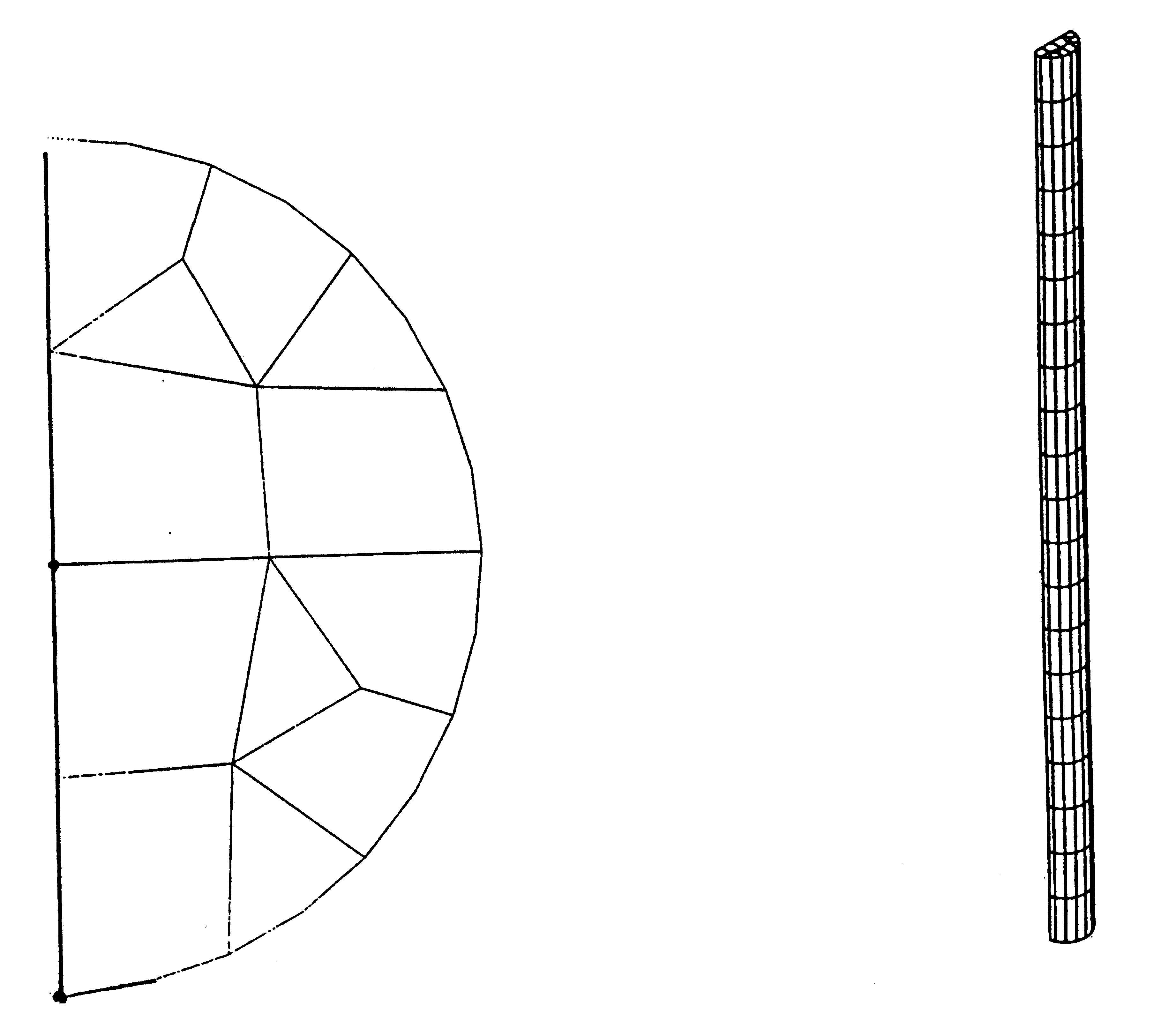
x, u
Point position: |
\(A,B\) in section \(z=0\) |
\(E,F\) in the middle section \(z=L/2\) |
|
Breakdown: |
20 elements depending on the length |
2 elements according to the radius, 8 elements according to the circumference. |
Since the load is symmetric, only half of the cylinder is modelled.
Boundary conditions:
recessed ends section (\(u=v=w=0\))
symmetry conditions in plane \(\mathrm{xz}\): \(v=0\)
Circumference pressure (field \(\mathrm{Up}\)) The surface of the cylinder is divided into 8 rows of elements according to the circumference (1 row of elements represents a sector of \(\pi /8\) radians. Since the pressure is in \(\mathrm{cos}\theta\), it is assumed to be uniform on each row. For any point on the corner surface \(\theta\), (between \({\theta }_{1}\) and and between and \({\theta }_{2}\), \({\theta }_{1}=(n–1)\frac{\pi }{8}\),, \({\theta }_{2}=n\frac{\pi }{8}\), \(1\le n\le 8\)), the pressure value assigned to the row of elements containing this point is taken to be equal to: \(\frac{\mathrm{p0}}{2}(\mathrm{cos}{\theta }_{1}+\mathrm{cos}{\theta }_{2})\). |
|
Vertical gravity next \(x\) (field \(\mathrm{Ug}\)) |
Node names:
\(A=\mathrm{N845}\) |
|
|
|
5.2. Characteristics of the mesh#
Number of knots: 1285
Number of meshes and types: 160 HEXA20, 80 PENTA15
5.3. Tested values#
Location |
Value type |
Reference |
Aster |
% difference |
Field \(\mathrm{Up}\) |
||||
Point E |
\(u(m)\) \(v(m)\) |
—7.82 x 10—6 10—21 |
||
Point \(F\) |
\(v(m)\) |
—7.816 x 10—6 10—21 |
||
Point \(B\) |
\({\sigma }_{\mathrm{yy}}(\mathrm{Pa})\) \({\sigma }_{\mathrm{zz}}(\mathrm{Pa})\) |
1.63 x 106 1.65 x 106 5.51 x 106 |
||
Field \(\mathrm{Up}+\mathrm{Ug}\) |
||||
Point \(E\) |
\(v(m)\) |
—7.46 x 10—6 10—21 |
||
Point \(F\) |
\(v(m)\) |
—7.44 x 10—6 10—21 |
||
Point \(B\) |
\({\sigma }_{\mathrm{yy}}(\mathrm{Pa})\) \({\sigma }_{\mathrm{zz}}(\mathrm{Pa})\) |
1.56 x 106 1.57 x 106 5.25 x 106 |
5.4. notes#
There are no reference values for this modeling. The results are to be compared with those of the AXIS_FOURIER \((A,B,D)\) models.
At point \(B\) (located in the plane of symmetry), we have: \({\sigma }_{\mathrm{rr}}={\sigma }_{\mathrm{xx}}\), \({\sigma }_{\theta \theta }={\sigma }_{\mathrm{yy}}\)