5. C modeling#
5.1. Characteristics of modeling#
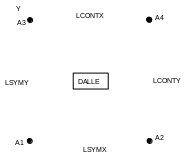

Q4GG modeling (TRIA3)
Boundary conditions:
. Side \(\mathrm{A2A4}\): \(\mathrm{DZ}=0\)
Symmetry conditions
. Side \(\mathrm{A1A2}\): \(\mathrm{DY}=\mathrm{DRX}=0\)
. Side \(\mathrm{A1A3}\): \(\mathit{DX}\mathrm{=}\mathit{DRY}\mathrm{=}0\)
M266 ROAD The slab is symmetric with respect to planes \((X\mathrm{=}0)\) and \((Y\mathrm{=}0)\), the calculations are carried out on a quarter of the slab.
X
5.2. Characteristics of the mesh#
Number of knots: 169
Number of meshes and type: 288 TRIA3
5.3. Tested sizes and results#
Identification |
Reference Type |
Reference |
Tolerance (%) |
\(\mathit{DZ}(\mathit{A1})\) |
“ANALYTIQUE” |
2.658 10-4 |
|
\(\mathit{MXX}(\mathit{A1})\) |
“ANALYTIQUE” |
|
|
\(\mathit{KXX}(\mathit{A1})\) |
“ANALYTIQUE” |
7.878 10-4 |
|
Identification |
Reference type |
Reference |
Tolerance (%) |
||
\(\mathit{MXX}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
4032.58 |
1.e-6 |
\(\mathit{KXX}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
7.8442 10-4 |
1.e-6 |
The quantities are expressed in the coordinate system defined by the nautical angles \(\alpha \mathrm{=}33°\) and \(\beta \mathrm{=}12°\).
Identification |
Reference Type |
Reference |
Tolerance (%) |
\(\mathit{DZ}(\mathit{A1})\) |
“ANALYTIQUE” |
2.658 10-4 |
|
\(\mathit{MXX}(\mathit{A1})\) |
“NON_REGRESSION” |
2836.04 |
1.e-6 |
\(\mathit{MYY}(\mathit{A1})\) |
“NON_REGRESSION” |
1195.36 |
1.e-6 |
\(\mathit{MXY}(\mathit{A1})\) |
“NON_REGRESSION” |
-1842.50 |
1.e-6 |
\(\mathit{KXX}(\mathit{A1})\) |
“NON_REGRESSION” |
5.5167 10-4 |
1.e-6 |
\(\mathit{KYY}(\mathit{A1})\) |
“NON_REGRESSION” |
2.3252 10-4 |
1.e-6 |
\(\mathit{KXY}(\mathit{A1})\) |
“NON_REGRESSION” |
-3.5840 10-4 |
1.e-6 |
Identification |
Reference type |
Reference |
Tolerance (%) |
||
\(\mathit{MXX}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
2836.04 |
1.e-6 |
\(\mathit{MYY}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
1195.36 |
1.e-6 |
\(\mathit{MXY}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
-1842.50 |
1.e-6 |
\(\mathit{KXX}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
5.5167 10-4 |
1.e-6 |
\(\mathit{KYY}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
2.3252 10-4 |
1.e-6 |
\(\mathit{KXY}\) |
\(\mathit{M266}\) |
\(\mathit{Point}1\) |
“NON_REGRESSION” |
-3.5840 10-4 |
1.e-6 |