1. Reference problem#
1.1. Geometry#
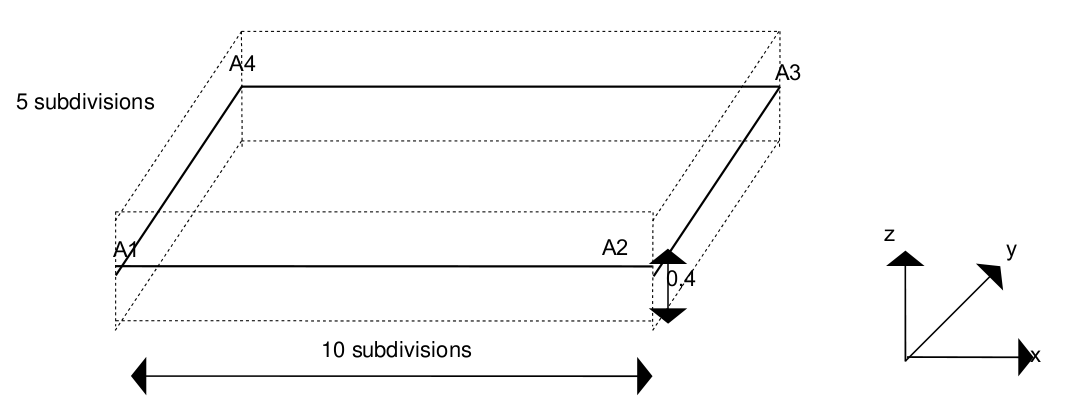
coordinates of the points (in \(m\)): \(\mathrm{A1}(\mathrm{0,0}\mathrm{,0})\) \(\mathrm{A2}(\mathrm{10,0}\mathrm{,0})\) \(\mathrm{A3}(\mathrm{10,5}\mathrm{,0})\) \(\mathrm{A4}(\mathrm{0,5}\mathrm{,0})\)
1.2. Material properties#
The material consists of 4 orthotropic layers with a thickness of 0.1.
The first layer is characterized by:
\(\mathrm{EL}={20000.10}^{6}\mathrm{Pa}\) |
|
|
|
the second layer by:
\(\mathrm{EL}={15000.10}^{6}\mathrm{Pa}\) |
|
|
|
the third layer by:
\(\mathrm{EL}={20000.10}^{6}\mathrm{Pa}\) |
|
|
|
and the fourth layer by:
\(\mathrm{EL}={15000.10}^{6}\mathrm{Pa}\) |
|
|
|
1.3. Boundary conditions and loads#
Node \(\mathrm{A1}\) is embedded:
\(\mathrm{dx}=0.\) |
|
|
\(\mathrm{dRx}=0.\) |
|
|
Node \(\mathrm{A2}\) is blocked according to the following ddls:
\(\mathrm{dx}=0.\) |
|
A modal force \(\mathrm{Fz}=-\mathrm{1000.N}\) is applied to node \(\mathrm{A3}\).