1. Reference problem

1.1. Geometry

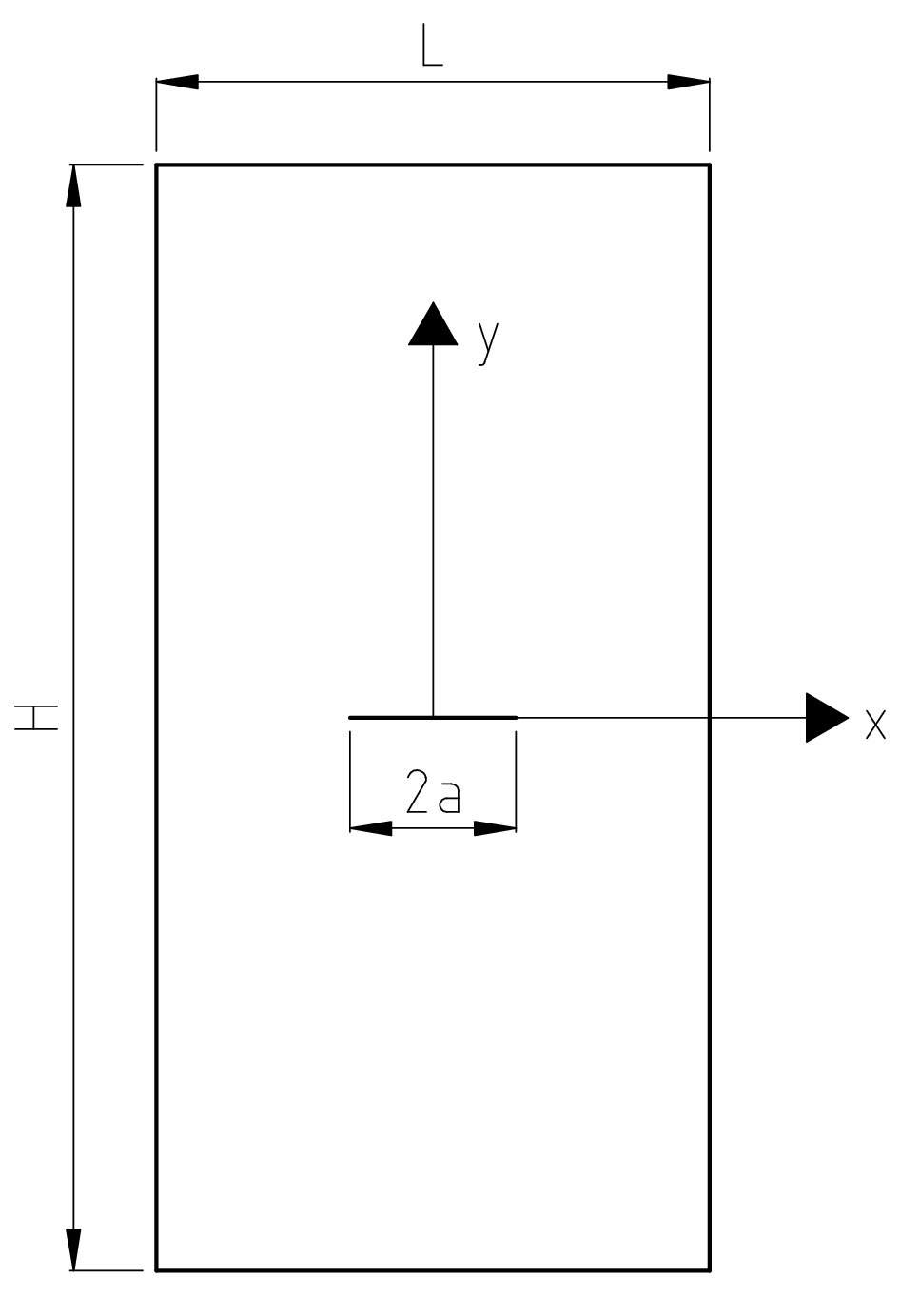
Figure 1.1-a : geometry of the cracked plate

Geometric dimensions of the cracked plate:

width	\(L=1000\mathrm{mm}\)
height	\(H=2000\mathrm{mm}\)

Initial crack length: \({\mathrm{2a}}_{0}=300\mathrm{mm}\).

The crack is positioned in the middle of the height of the plate (\(H/2\)).

1.2. Material properties

Young’s module \(E=206000\mathrm{MPa}\)

Poisson’s ratio \(\nu =0.33\)

1.3. Boundary conditions and loads

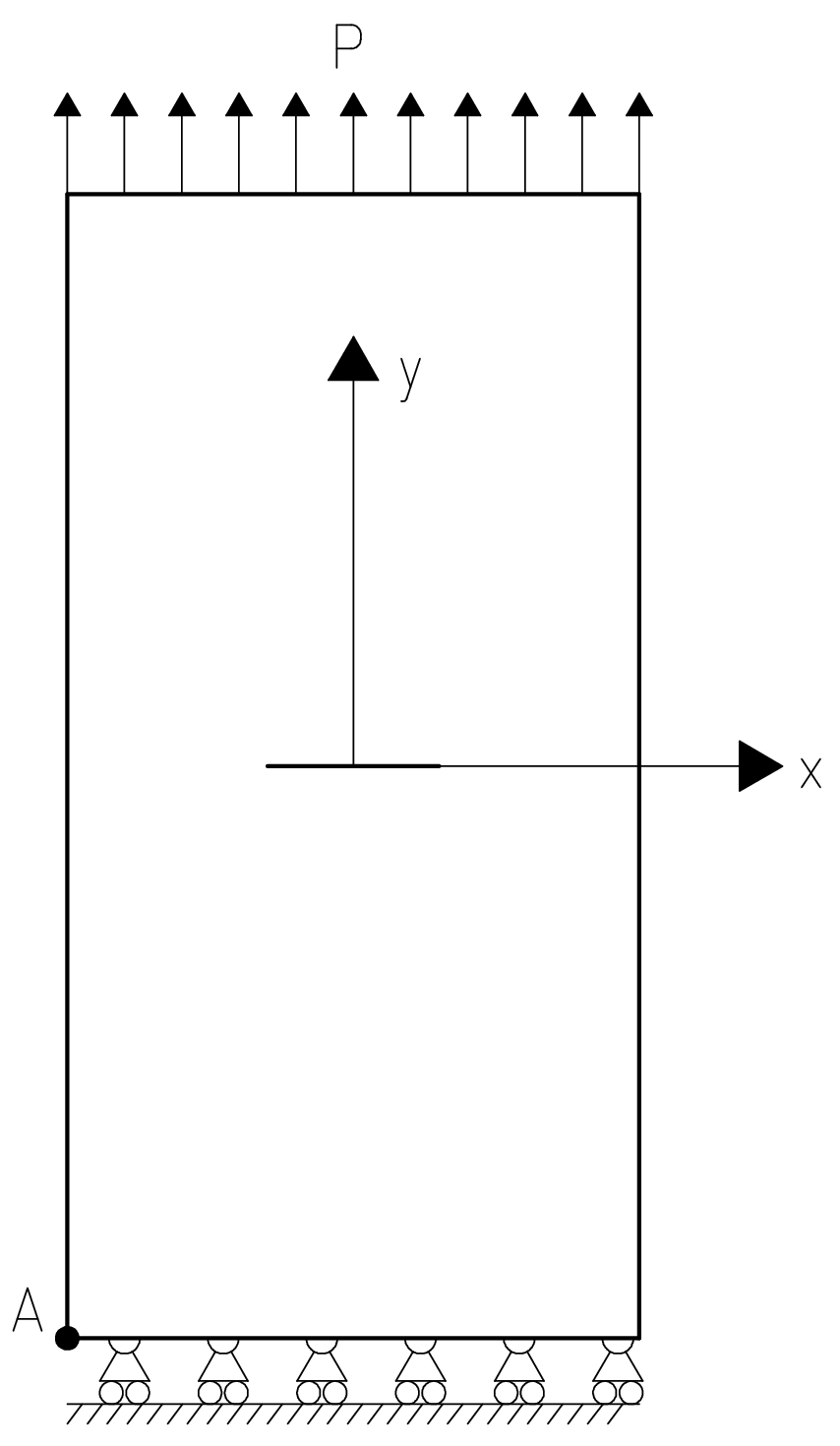
Figure 1.3-a : boundary conditions and loads

Boundary conditions:

Point \(A\): \(\Delta X=\Delta Y=0\)

Lower end of plate points: \(\Delta Y=0\)

Loading:

Pressure applied to the upper end of the plate: \(P=1\mathrm{MPa}\)

Three propagations are calculated by imposing a crack advance equal to \(30\mathrm{mm}\) at each crack bottom. As a result of the symmetry of the geometry, the boundary conditions and the loading, the advances of the two bottoms of the crack are always equal to the imposed advance.