1. Reference problem#

1.1. Geometry#

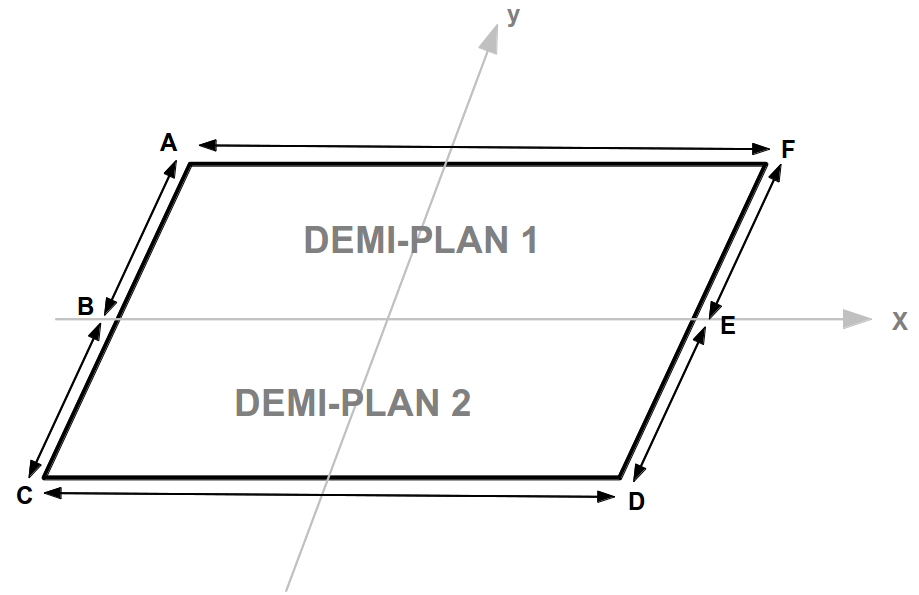
Figure 1.1 Problem geometry

Length: \(L=20\mathit{cm}\)

Width: \(l=20\mathit{cm}\)

\(\mathit{AC}=\mathit{CD}\)

Material for half plane 1:

Young’s module	\(E=2\times {10}^{12}\mathit{Pa}\)
Poisson’s Ratio	\(\nu =0.3\)

Material for half plane 2:

Young’s Module	A, D Modeling: \(E=8\times {10}^{12}\mathit{Pa}\) B, E modeling: \(E=2\times {10}^{12}\mathit{Pa}\) C, F modeling: \(E=5\times {10}^{11}\mathit{Pa}\)
Poisson’s Ratio	\(\nu =0.3\)

For models A, B and C:

Imposed displacement:

Embedding sides \(\mathit{AB}\), \(\mathit{BC}\)	\(\mathit{DX}=0\)
Embedding point B:	\(\mathit{DY}=0\)
Uniform connection on the side: \(\mathit{DE}\)	\({U}_{X}({N}_{i})={U}_{X}({N}_{1})\)
Uniform connection on the side: \(\mathit{EF}\)	\({U}_{X}({N}_{i})={U}_{X}({N}_{1})\)

For D, E, and F models:

Imposed displacement:

Embedding point B:	\(\mathit{DX}=0\), \(\mathit{DY}=0\)
Embedding point E:	\(\mathit{DY}=0\)

For A, B, C, D, E, and F models:

Imposed loading:

Force contour on the side \(\mathit{CD}\)	\({F}_{X}=-75\times {10}^{6}N\)
Force contour on the side \(\mathit{FA}\)	\({F}_{X}=75\times {10}^{6}N\)

\(c\): characteristic length of the horizontal crack.

\(a\): characteristic length of the deflected crack a \(45°\).