1. Reference problem#
1.1. Geometry#
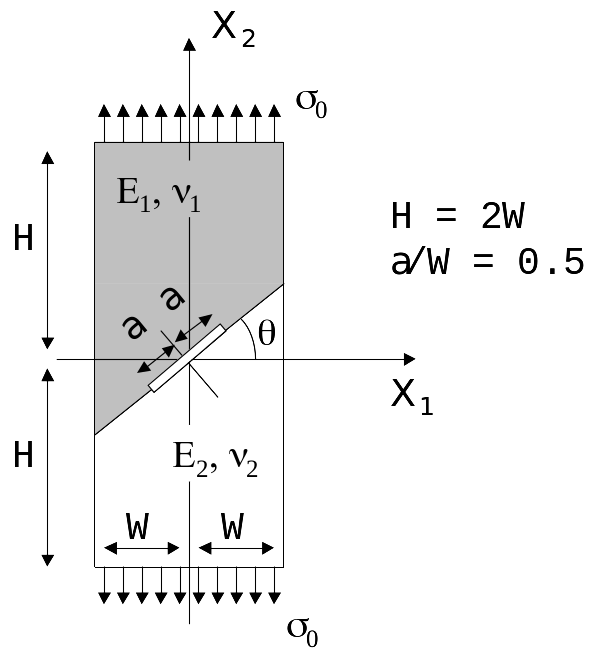
We consider 4 values of angle \(\theta\): 15°, 30°, 45° and 60°.
The other dimensions are chosen such as \(H=\mathrm{2W}=\mathrm{4a}\).
The value of \(a\) is \(1.E-3m\).
1.2. Material properties#
Material #1
Elastic, linear, isotropic, Young’s modulus \({E}_{1}\mathrm{=}2E+12\mathit{Pa}\) and Poisson’s ratio \({\nu }_{1}\mathrm{=}\mathrm{0,3}\).
Material #2
Elastic, linear, isotropic, Young’s modulus \({E}_{2}=2E+11\mathrm{Pa}\) and Poisson’s ratio \({\nu }_{2}=\mathrm{0,3}\).
1.3. Boundary conditions and loading#
Rigid modes are blocked by the following boundary conditions:
\(\mathrm{UX}=\mathrm{UY}=0\) at the bottom left corner of the template.
\(\mathrm{UY}=0\) on the bottom edge.
Charging: uniform tension \({\sigma }_{\mathrm{yy}}={\sigma }_{0}\) on the top edge.
The value of \({\sigma }_{0}\) is \(100\mathrm{MPa}\).