1. Reference problem#

1.1. Geometry#

Geometry is a square with side \(L=100\mathrm{mm}\).

The material is incompressible elastic and has the following properties:

\(E=100\mathrm{MPa}\)

\(\nu =0.4999\)

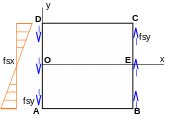
Given the antisymmetric nature of the problem, only half of the massif is modelled with the following boundary conditions:

On \(\mathrm{OE}\):

\(\mathrm{DX}(\mathrm{OE})=0\)

On \(\mathrm{OD}\):

\(\mathrm{DX}(O)=\mathrm{DY}(O)=0\)

\(\mathrm{DX}(D)=0\)

\(\mathrm{fsx}=\frac{\mathrm{8y}}{L}\mathrm{.}{\sigma }_{d}\)

\(\mathrm{fsy}=-(1-\frac{{\mathrm{4y}}^{2}}{\mathrm{L²}})\mathrm{.}{\sigma }_{d}\)

On \(\mathrm{BC}\):

\(\mathrm{fsy}=+(1-\frac{{\mathrm{4y}}^{2}}{\mathrm{L²}})\mathrm{.}{\sigma }_{d}\)

With \({\sigma }_{d}\) a given constraint, which we will take equal to 1 in the test. \({\sigma }_{d}=1\mathrm{MPa}\)