1. Reference problem#
1.1. Geometry#
Straight beam of length \(L\), direction \(x\). Dimensions are in meters, \(\text{[m]}\).
Three different types of cross sections are calculated simultaneously:
1 rectangular section |
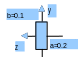
|
1 angle section with equal wings |
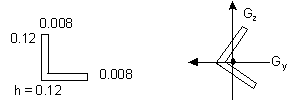
|
1 circular section |

|
1.2. Material properties#
Young’s module: \(E\mathrm{=}2.{10}^{11}\mathit{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
1.3. Boundary conditions and loads#
1.3.1. Recessed case-free, unit loads at the end#
The length of the beam is \(L=2m\).
Embedding in \(O\).
Six unit loads in \(B\):
\(\mathrm{Fx}=1\) |
|
\(\mathrm{Fy}=1\) |
|
\(\mathrm{Fz}=1\) |
|
Combined flexure plus traction loading: \(\mathrm{Fx}=1\); \(\mathrm{My}=1\); \(\mathrm{Mz}=1\);
A load combined with shear forces plus twisting: \(\mathrm{Fy}=1\) \(\mathrm{Fz}=1\) \(\mathrm{Mx}=1\).
1.3.2. Simple support cases, unit loads at the end#
The length of the beam is \(L=6m\).
A linear distributed load: \(\mathit{Fy}=1000\mathrm{.}x\) circular section, with radius \(0.1m\) (F, G, H, I models) (with simple support in \(O\) and \(B\) in this case).
1.4. Notation of cross-sectional characteristics#
The geometric characteristics of the cross sections are noted:
\(A\) |
area of the section |
\({I}_{y},{I}_{z}\) |
geometric moments of inertia with respect to the main axes of inertia of the section |
\(\mathrm{JX}\) |
torsional constant |
\(\mathrm{ay},\mathrm{az}\) |
shear coefficients in the \(\mathit{Gy}\) and \(\mathit{Gz}\) directions |
\({A}_{y}^{\text{'}}=\frac{A}{\mathrm{ay}}\) and \({A}_{z}^{\text{'}}=\frac{A}{\mathrm{az}}\) |
reduced areas equivalent to the shear force |
\({e}_{y},{e}_{z}\) |
eccentricity of the center of torsion |
\(\mathrm{JG}\) |
warping constant |