2. Modeling A#

2.1. Meshing#

The mesh of the three parts of the pump is provided, as well as its complete mesh. After importing the meshes into SALOME - MECA, we will take the time needed to find the names of the groups needed for the data layout.

The mesh is made of 3S solid elements in DKT plate elements. The plate elements correspond to a thickness of:

  • \(30\mathit{mm}\) for the tier (“Pal_2D” group)

  • \(50\mathit{mm}\) for volute (group “Vol_2D”)

  • \(10\mathit{mm}\) for the pipe (group “Vol_2D”)

2.2. Aster command file#

The main steps of the calculation with Aster are, for each substructure, the usual data processing steps:

Reading the mesh in MED format (LIRE_MAILLAGE (“FORMAT =” MED”)).

Definition of the finite elements used (AFFE_MODELE). “3D” and “DKT” modeling

Material definition and assignment (DEFI_MATERIAU and AFFE_MATERIAU).

Assigning the characteristics of plate elements (AFFE_CARA_ELEM).

Assigning boundary conditions (AFFE_CHAR_MECA).

Then the construction of the macro-elements, their assembly, the modal calculation of the assembled structure, the construction of the skeleton, the restoration of the modal calculation on the skeleton and, finally, the impression of the modes:

Creation of substructures (CREA_ELEM_SSD)

Assembling the substructures (ASSE_ELEM_SSD)

Modal calculation (CALC_MODES)

Construction of the global mode visualization skeleton (DEFI_SQUELETTE)

Restitution on the skeleton (REST_SOUS_STRUC)

Fashion printing in MED format (IMPR_RESU)

The aim is to specify the type of substructure to be used when creating substructures. Here we have:

TYPE =” CLASSIQUE “

2.3. Results#

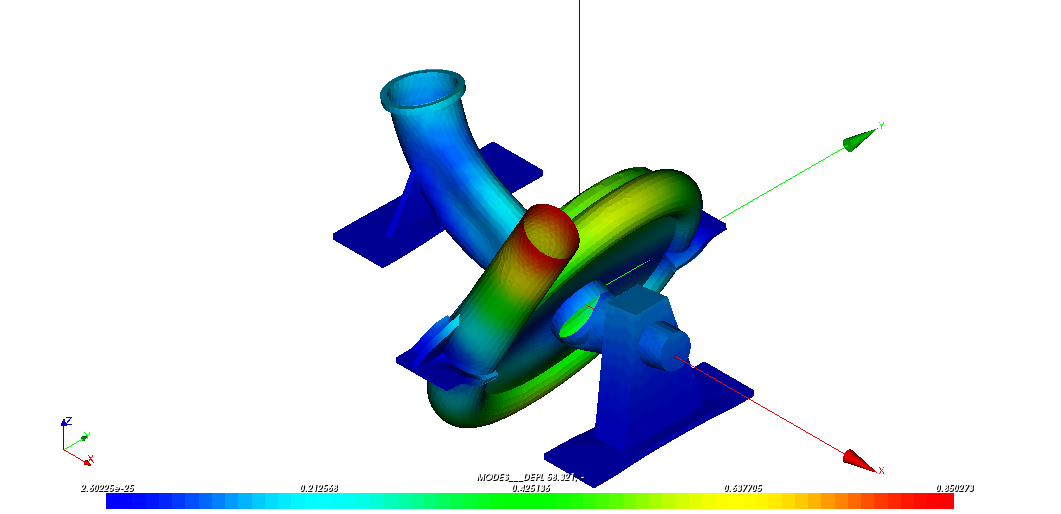
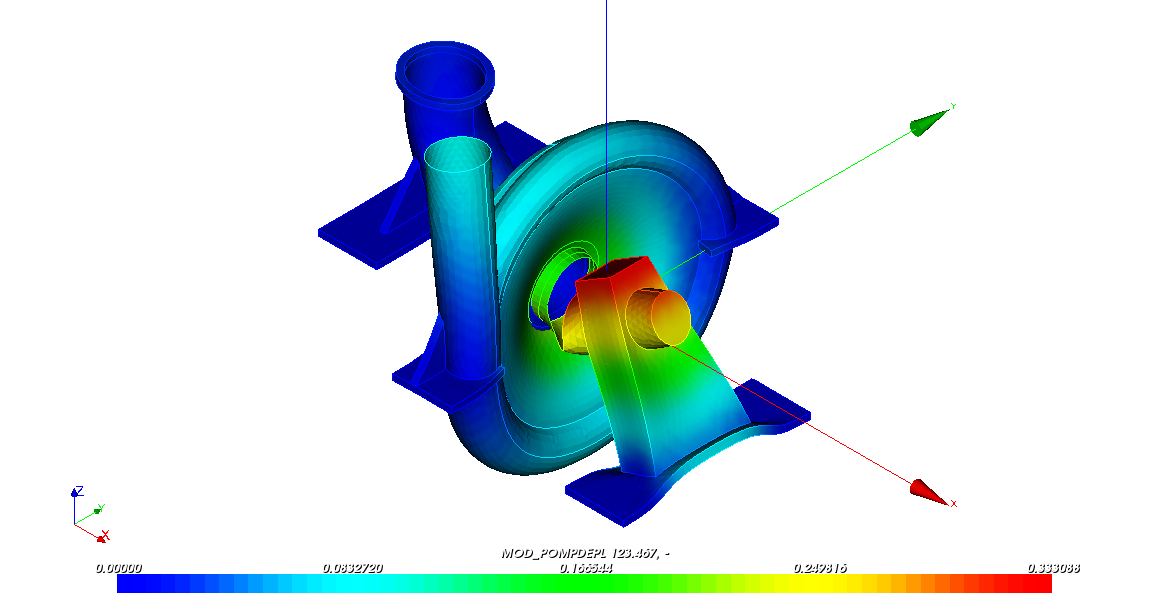
The quantities compared are the frequencies of the first 10 natural modes of the pump obtained during the direct calculation carried out on the global mesh with those obtained by substructuring on the pump divided into three parts.

Mode

Direct modal calculation (Hz)

Calculation by SSD (Hz)

1

58.32

58.32

2

123.47

123.55

3

155.27

155.31

4

190.57

190.77

5

224.85

225.71

6

230.77

232.99

7

249.22

252.73

8

259.38

260.00

9

261.07

262.40

10

278.07

284.77

It can be seen that the frequencies calculated by the two methods are very similar.

We can also verify in SALOME - MECA that this is also the case for modal deformations.

_images/100000000000042500000202230B6AFD38CC2D2A.png

Figure 3: Mode 1 of the direct modal calculation

 _images/100000000000042500000202A8AFDE3A9CDA83A9.png

Figure 4: Mode 1 of the SSD calculation by Craig and Bampton
_images/100000000000049200000257F83CDBCF80AF9003.png

Figure 5: Mode 2 of the direct modal calculation

 _images/10000000000004920000025731573AF31BB503EA.png

Figure 6: Mode 2 of the SSD calculation by Craig and Bampton
_images/10000000000004920000025729C7695E97782ED8.png

Figure 7: Mode 3 of the direct modal calculation

 _images/100000000000049200000257FE12AF66C3F9A028.png

Figure 8: Mode 3 of the SSD calculation by Craig and Bampton

On the other hand, the classical dynamic substructuring method of Craig & Bampton is relatively expensive. In the next part we propose to use the interface method. Although slightly more complex, by limiting the number of methods of connection between the substructures, it significantly increases the efficiency of the substructuring technique.