3. C modeling#

3.1. Problem description#

The objective of this modeling is the use of the macro command CALC_MODES [U4.52.02] with the option “BANDE” divided into several sub-bands. This command allows you to start a succession of real eigenmode calculations.

The following actions are carried out:

  • Obtaining modes by simultaneous iterations, in specified frequency bands,

  • Application of a standard, filtering according to a criterion of modal parameter value greater than a certain threshold and finally concatenation of the calculated data structures into a single one.

The modes are calculated by the CALC_MODES [U4.52.02] command with the “BANDE” option and normalized by the NORM_MODE [U4.52.11] command. The calculated modes are filtered and concatenated using the EXTR_MODE [U4.52.12] command.

3.1.1. Objective#

The objective of this modeling is:

  • To « weigh » the finite element model and to evaluate the number of modes,

  • To use the macro command CALC_MODES with the option “BANDE” divided into several sub-bands to calculate the natural frequencies.

3.1.2. Geometry#

You can retrieve the mesh in the test case directory.

The thickness of the shell is \(e=\mathrm{0,3045}m\)

_images/100000000000017C0000021453622D804808AE39.png

3.1.3. Material Properties#

The material is linear isotropic elastic:

  • Young’s module \(E=\mathrm{2,76}\mathrm{.}{10}^{10}N/{m}^{2}\),

  • Poisson’s ratio \(\nu =\mathrm{0,166}\),

  • density \(\rho =2244\mathrm{Kg}/{m}^{3}\)

3.1.4. Boundary conditions and loading#

The tower is embedded at its base.

3.2. Characteristics of modeling#

3.2.1. Characteristics of the mesh#

The mesh is composed of 1860 QUAD4 and 1860 knots

The tower is modelled with shell elements DKT

3.2.2. Aster commands#

The main steps of the calculation with*Aster* will be:

Reading the mesh (LIRE_MAILLAGE).

Definition of the finite elements used (AFFE_MODELE). We will assign modeling DKT to all the elements of the tower.

Material definition and assignment (DEFI_MATERIAU and AFFE_MATERIAU).

The mechanical characteristics are identical throughout the structure.

Assigning shell element characteristics (AFFE_CARA_ELEM).

The thickness of all the elements is the same.

Assigning boundary conditions (AFFE_CHAR_MECA).

Calculation of elementary stiffness matrices (CALC_MATR_ELEM ((OPTION =” RIGI_MECA “)).

Calculation of elementary mass matrices (CALC_MATR_ELEM ((OPTION =” MASS_MECA “).

Numbering the unknowns of a system of linear equations (NUME_DDL)

Assembly of elementary mass and stiffness matrices (ASSE_MATRICE).

Note: to go faster we can use the macro ASSEMBLAGE to build the matrices!

Question #1:

  • Weigh the model (POST_ELEM) and assess the number of modes whose frequency is less than \(4\mathrm{Hz}\) (INFO_MODE).

Question #2:

  • Calculate the natural frequencies and the first associated modes present in the frequency band \(0.\mathrm{Hz}\) to \(4\mathrm{Hz}\) (CALC_MODES)

  • Normalize with the infinite norm, on all components of physical nodes while requiring the calculation of effective unit masses (NORM_MODE, EXTR_MODE).

  • Print the proper modes (IMPR_RESU) in MED format for viewing in Salome.

Question #3:

  • Calculate the natural frequencies by grouping the three operations CALC_MODES, NORM_MODE and EXTR_MODE into one (by cutting into 2 intervals) with CALC_MODES and the option “BANDE” divided into several sub-bands.

Question #4:

  • Calculate the natural frequencies by grouping the three operations CALC_MODES, NORM_MODE and EXTR_MODE into one (by cutting into 4 intervals) with CALC_MODES and the option “BANDE” divided into several sub-bands.

Question #5:

  • We achieve the same thing as that asked in question 4 but with the method of LANCZOS.

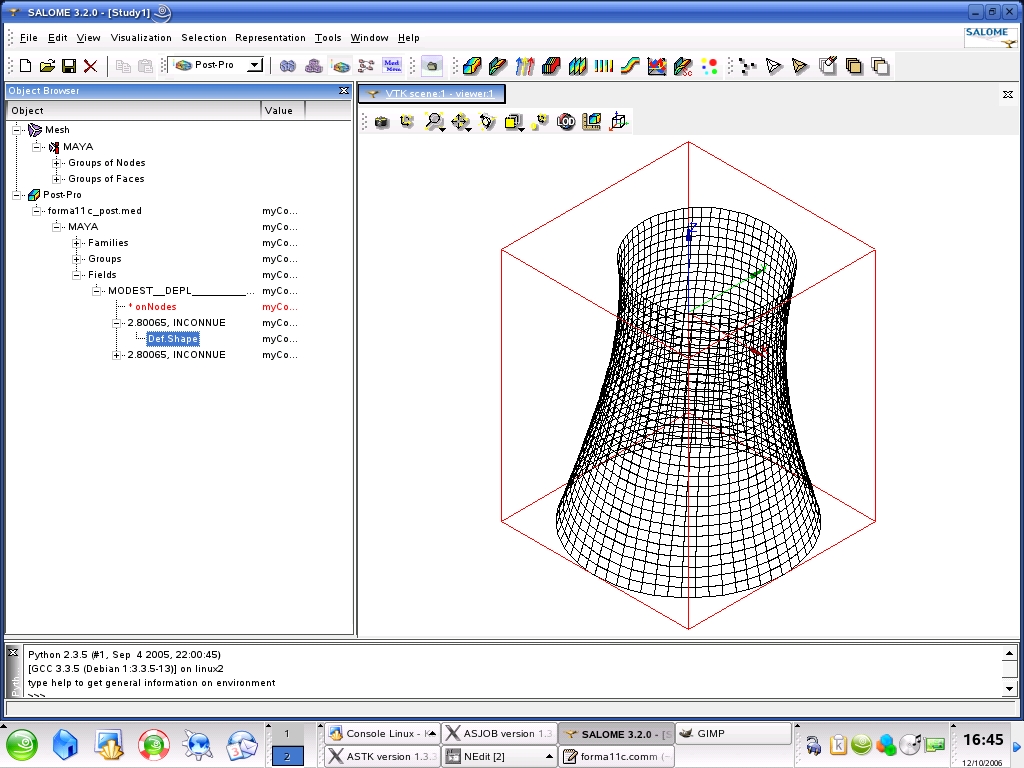
3.3. Help with post-treatment under Salome#

The different steps for visualizing modal deformations with Salomé are as follows:

Start Salome on Linux

Start the Mesh/New mesh module

Click on File/Import/ MED file and select the med file containing the mesh

Start the Post-Pro post-processing module

Click on File/Import/ MED file and select the med file containing the specific modes to be viewed

Deploy the Post-Pro line tree completely in the Object Browser in order to see all the movement fields in detail.

Click on one of the fields and with the right mouse button click on Deformed Shape. (modal distortion is displayed).

Deploy the line containing the visualized field, then click on Def. Shape and then click on the right mouse button and select Sweeper to animate the deformation.
_images/1000000000000400000003000B8228F8652F74DA.jpg

3.4. notes#

Best practices: you must first:

Weigh your model with POST_ELEM,

Evaluating the spectrum with INFO_MODE.

The CALC_MODES command, with the “BANDE” option divided into several sub-bands, is more economical to search for a large spectrum.

As long as you don’t overcook it,

It is necessary to verify the agreement of the identified bits of spectrum,

Saving time can be very important: \(\text{500\%}\),

You can easily and automatically add other operations to it: normalization, filtering, concatenation of data structures.

3.5. Tested sizes and results#

Mode

Frequency in \(\mathrm{Hz}\)

1

\(2.80065\mathrm{Hz}\)

2

\(2.80065\mathrm{Hz}\)
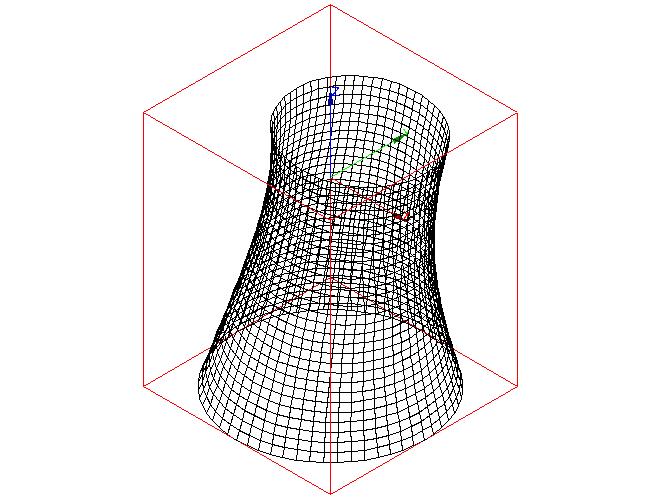
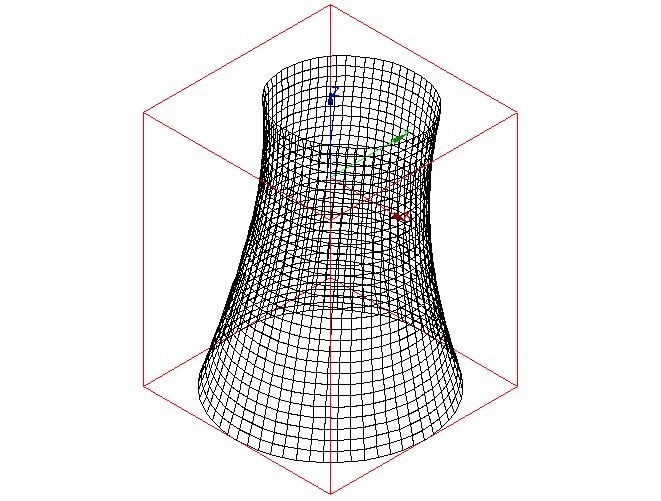
_images/1000000000000295000001F57D06744D4D0F73A5.jpg _images/1000000000000295000001F5D798BF1F7ED9088F.jpg

Modal warp ( \(2.80065\mathrm{Hz}\) ) Modal warp ( \(2.80065\mathrm{Hz}\) )