2. B modeling#

2.1. Problem description#

2.1.1. Objective#

The objective of this modeling is to determine for a free free sphere-type structure, (presence of multiple rigid body modes):

  • Natural frequencies located in a frequency band using the SORENSEN method,

  • Natural frequencies located in a frequency band using the LANCZOS method with or without rigid mode (OPTION = MODE_RIGIDE),

  • The 16 smallest natural frequencies with the SORENSEN method

2.1.2. Geometry#

_images/Shape1.gif

2.1.3. Material properties#

The material is linear isotropic elastic:

  • Young’s module \(E={10}^{8}N/{m}^{2}\),

  • Poisson’s ratio \(\nu \mathrm{=}0.3\),

  • density \(\rho ={10}^{4}\mathrm{kg}/{m}^{3}\)

2.1.4. Boundary conditions and loading#

None

2.2. Characteristics of modeling#

2.2.1. Characteristics of the mesh#

_images/10000000000001D5000001C8A161BBABF40381B9.png

The mesh includes 160 HEXA20 stitches, and 813 knots.

Solid elements (3D) will be used for modeling.

2.2.2. Aster commands#

The main steps of the calculation with*Aster* will be:

Reading the mesh (LIRE_MAILLAGE).

Definition of the finite elements used (AFFE_MODELE).

Material definition and assignment (DEFI_MATERIAU and AFFE_MATERIAU).

The mechanical characteristics are identical throughout the structure.

Calculation of elementary stiffness matrices (CALC_MATR_ELEM ((OPTION =” RIGI_MECA “)).

Calculation of elementary mass matrices (CALC_MATR_ELEM ((OPTION =” MASS_MECA “)

Numbering the unknowns of the system of linear equations (NUME_DDL)

Assembly of elementary mass and stiffness matrices (ASSE_MATRICE).

**Note:* to go faster we can use the macro ASSEMBLAGE to build the matrices!

Question #1:

  • Calculate with the SORENSEN method (under the keyword factor SOLVEUR_MODAL), the frequencies located in the \((0.\mathrm{Hz},2880\mathrm{Hz})\) frequency band as well as the associated modes (CALC_MODES).

  • If the calculation fails we can extend the frequency band by a slightly negative margin.

  • Print the proper modes (IMPR_RESU) in MED format for viewing in Salome.

Question #2:

  • Calculate with the LANCZOS method with or without option MODE_RIGIDE the frequencies located in the \((0.\mathrm{Hz},2880\mathrm{Hz})\) frequency band as well as the associated modes (CALC_MODES).

Question #3:

  • Calculate with the SORENSEN method the 16 smallest frequencies as well as the associated modes (CALC_MODES). We can use the parameter PREC_SHIFT (under the keyword factor CALC_FREQ) to get around the problem of zero frequencies.

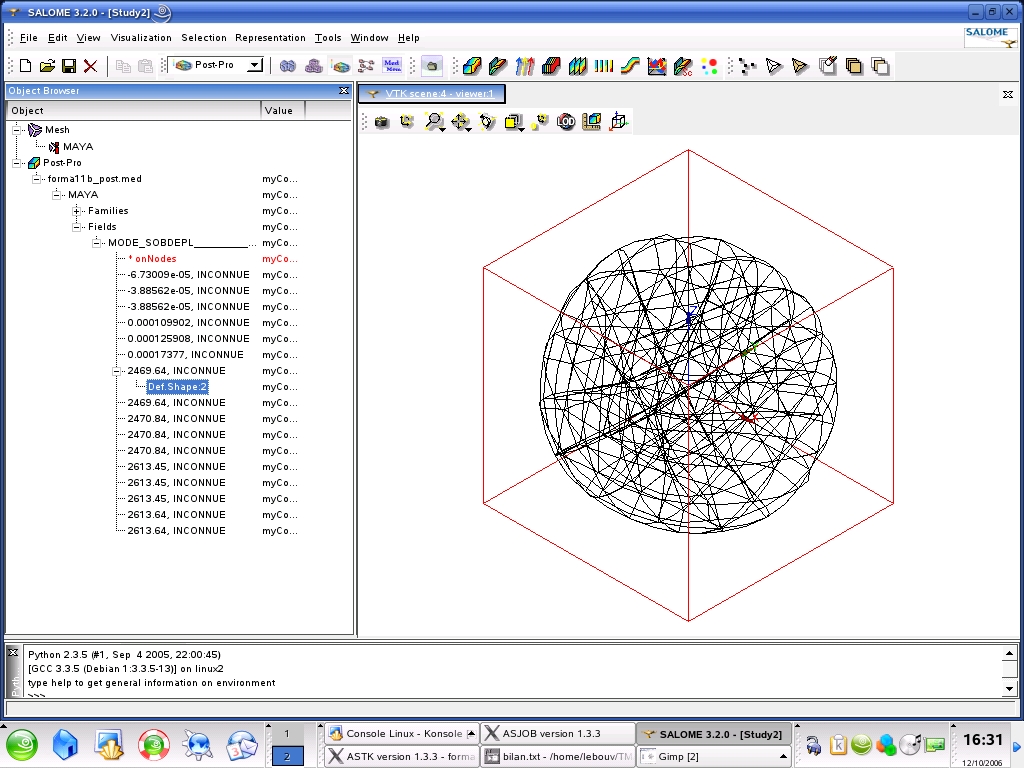
2.3. Help with post-treatment under Salome#

The different steps for visualizing modal deformations with Salomé are as follows:

Start Salome on Linux

Start the Mesh/New mesh module

Click on File/Import/ MED file and select the med file containing the mesh

Start the Post-Pro post-processing module

Click on File/Import/ MED file and select the med file containing the specific modes to be viewed

Deploy the Post-Pro line tree completely in the Object Browser in order to see all the movement fields in detail.

Click on one of the fields and with the right mouse button click on Deformed Shape. (modal distortion is displayed).

Deploy the line containing the visualized field, then click on Def. Shape and then click on the right mouse button and select Sweeper to animate the deformation.
_images/100000000000040000000300E72A0F7C1FFC478A.jpg

2.4. notes#

The factorization of the \({(K-\sigma \text{})}^{-1}={\mathrm{LDL}}^{T}\) shifted matrices governed by the parameterization: NMAX_ITER_SHIFT, SOLVEUR/NPREC [U4.50.01] and PREC_SHIFT, can only be done if they are regular.

This is often a problem when the magnitude of the terms in \(K\) is greater than the magnitude of the terms in \(M\) and \(\sigma\) is a good approximate eigenvalue. The operator’s policy is to issue a ALARME when it is a Sturm test and a ERREUR_FATALE when it comes to the operator’s work matrix. In case of problems, you can always change options or shift.

Detecting rigid body modes is often a problem for classical modal solvers! The best practice is to use the SORENSEN method using a frequency band whose lower bound is zero or even slightly negative. The solver normally captures them without any problem (they are just multiple modes that are a bit particular). Otherwise, with TRI_DIAG, the MODE_RIGIDE option is recommended.

2.5. Tested sizes and results#

The results obtained with the SORENSEN method and the LANCZOS method with and without the OPTION = MODE_RIGIDE option are shown in the table below.

CALC_MODES

Sorensen method (METHODE =” SORENSEN “)

Lanczos method (with the option MODE_RIGIDE )

Lanczos method (without the option MODE_RIGIDE )

Fashion

Frequency

Fashion

Frequency

Fashion

Frequency

5555

-3.88562E-05

6666

0.00000E+00

4444

1.22874E-04

4444

-3.88562E-05

5555

0.00000E+00

5555

2.70602E-04

3333

-6.73009E-05

4444

0.00000E+00

3333

-5.03634E-04

2222

1.09902E-04

3333

0.00000E+00

2222

-5.69081E-04

6666

1.25908E-04

2222

0.00000E+00

6666

4.46762E-03

1111

1.73770E-04

1111

0.00000E+00

7777

2.46964E+03

7777

2.46964E+03

7777

2.46964E+03

8888

2.46964E+03

8888

2.46964E+03

8888

2.46964E+03

9999

2.47084E+03

9999

2.47084E+03

9999

2.47084E+03

10

2.47084E+03

10

2.47084E+03

10

2.47084E+03

1111

2.47084E+03

1111

2.47084E+03

1111

2.47084E+03

12

2.61345E+03

12

2.61345E+03

12

2.61345E+03

13

2.61345E+03

13

2.61345E+03

13

2.61345E+03

14

2.61345E+03

14

2.61345E+03

14

2.61345E+03

15

2.61364E+03

15

2.61364E+03

15

2.61364E+03

16

2.61364E+03

16

2.61364E+03

16

2.61364E+03

17

3.48770E+03
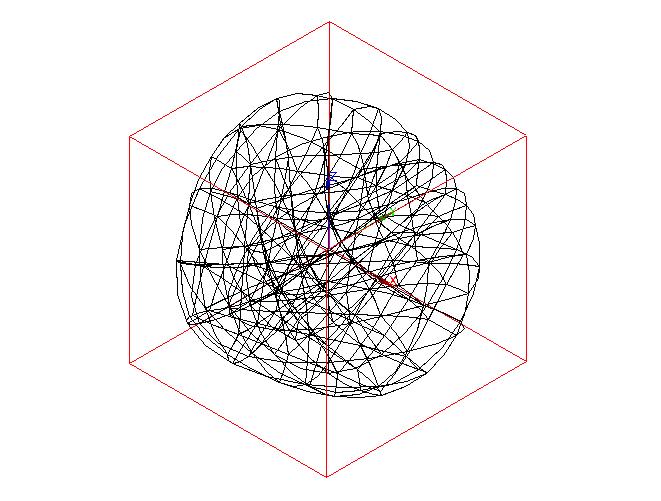
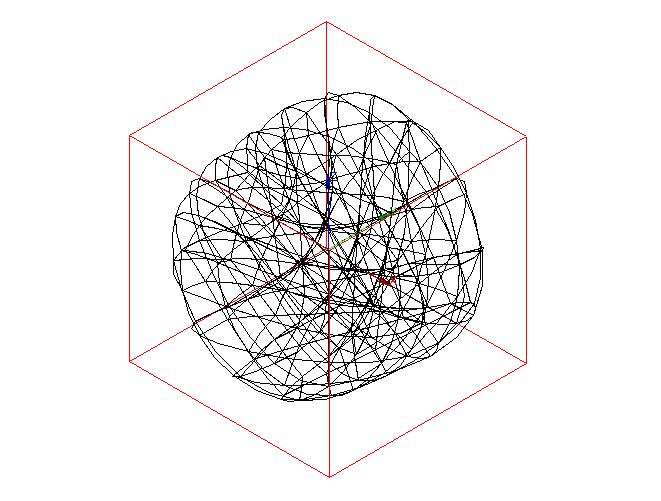
_images/1000000000000295000001F5189058E08B1CD6F6.jpg _images/1000000000000295000001F513A22AB69C107FFB.jpg

Modal warp ( \(2469.64\mathrm{Hz}\) ) Modal warp ( \(2469.64\mathrm{Hz}\) )

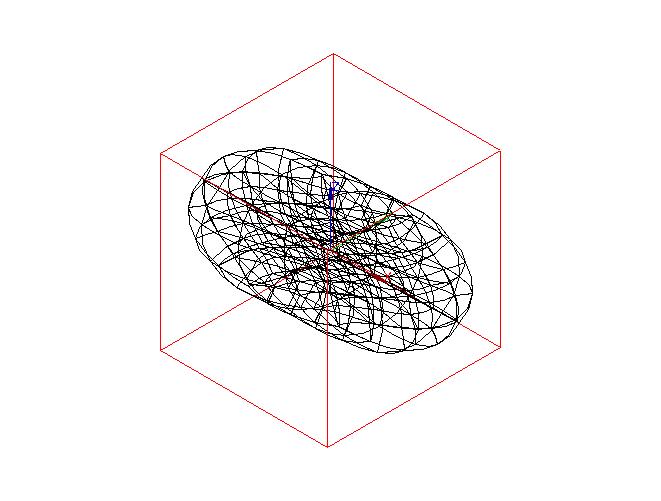
_images/1000000000000295000001F51FB3B0C0759A6266.jpg

Modal deformed ( \(2470.84\mathrm{Hz}\) )