1. Reference problem#

1.1. Geometry#

The system considered in the 3D case is that of an elastic bar with a square cross section. A displacement along \(x\) is imposed on one of the vertical faces and the propagation of a compression wave is observed. The lateral surface of the bar is left free. The absorbent elements are placed on the face opposite to the excitation face in order to simulate the infinite nature of the bar in this direction. In the 2D case, the principle is identical with a bar that is supposed to be very wide, of which only one vertical section is modelled (see diagram).

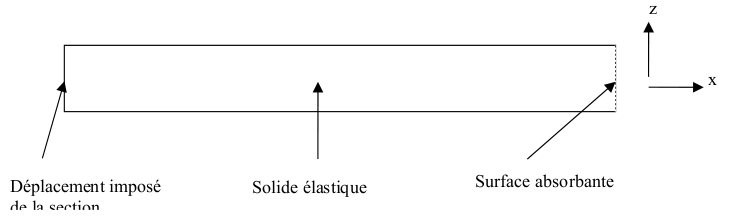
_images/10000000000002DF000000DAFEBD8E3EB4CFDDA5.png

3D case section:

2D case section:

_images/10000000000002360000009959BA19F10E7F3A36.png

1.2. Material properties#

Bar: concrete

Density:

\(2400{\mathrm{kg.m}}^{-3}\)

Young’s module:

\(\mathrm{3,6}{.10}^{10}\mathrm{Pa}\)

Poisson’s ratio:

\(\mathrm{0,48}\)

Note

This test is also used to check the dependence of the material of the absorbent elements on the coordinates. We therefore use the following formula for Young’s modulus: \(3.6\cdot {10}^{10}\times x/200\) with \(x=200\) on these elements.

1.3. Boundary conditions and loads#

All the nodes on the face of the piston in contact with the fluid are forced to move according to \(x\) with the following temporal excitation function:

_images/10000000000003E00000022D6E78AF3E32B7A9E3.png

1.4. Initial conditions#

The displacement is zero throughout the bar at the initial instant.