1. Reference problem#
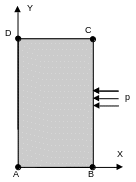
1.1. Geometry#
Coordinates of points expressed in meters:
\(A:(0.0,0.0)\)
\(B:(0.35,0.0)\)
\(C:(0.35,0.6)\)
\(D:(0.0,0.6)\)
1.2. Elastic properties of the material#
\(E=1.8\times {10}^{11}\mathrm{Pa}\) Young’s module
\(\nu =0.3\) Poisson’s Ratio
\(\rho =7800.0{\mathrm{kg.m}}^{-3}\) Density
\(\alpha =3\times {10}^{-5}s\)
\(\beta =0.001{s}^{-1}\)
The coefficients \(\alpha\) and \(\beta\) make it possible to build a viscous damping matrix that is proportional to the stiffness and to the mass \([C]=\alpha [K]+\beta [M]\).
1.3. Boundary conditions and loads#
Embedding on the \(\mathit{AD}\) side
\(\mathrm{DX}=0.0m\), \(\mathrm{DY}=0.0m\)
The \(\mathit{BC}\) side is subject to a harmonic pressure of amplitude \(p\mathrm{=}{10}^{5}\mathit{Pa}\) at a frequency \(f=1500\mathrm{Hz}\)