2. Benchmark solution#
2.1. Calculation method and reference results#
For the free vibrations of a thin cylindrical pipe, the reference solution adopted is that obtained in [bib1] by Haar wavelet discretization method (HWDM). The Goldenveizer-Novozhilov shell theory is suitable for formulating this problem. Theoretically, the solution consists of infinite terms in Haar wavelet series. However, finite terms are practically considered in the current calculation and the convergence of the results is shown in [bib7] with J=7 (maximum level of resolution).
For the case described in the previous paragraph., the reference frequencies for natural modes are given in [bib1] via a frequency parameter, \(\mathrm{\lambda }\), as follows (\(m\) and \(n\) are the wave numbers in the axial and circumferential directions, numerical results are noted in columns HWDM):
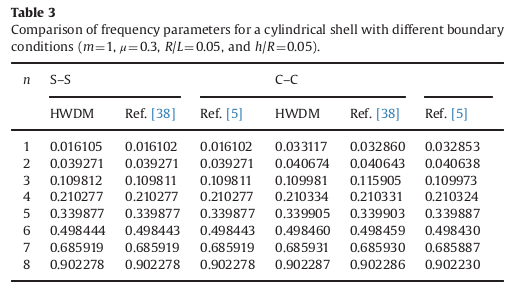
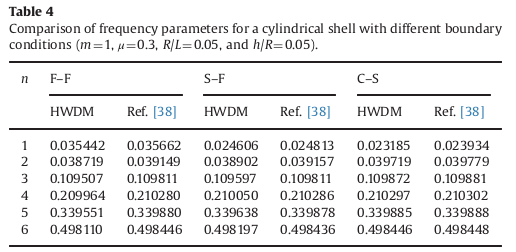
Fig. 2. Benchmark results in [bib1]
This frequency parameter \(\mathrm{\lambda }\) is defined by:
\(\mathrm{\lambda }=\mathrm{\omega }R\sqrt{\mathrm{\rho }(1-{\mathrm{\mu }}^{2})/E}\)
where \(\mathrm{\omega }\) is the natural frequency (unit: rad/s).
Therefore, we can obtain a frequency table in Hz (\(f=2\mathrm{\pi }\mathrm{\omega }\)) with geometry and material properties for our case:
Tab. 1. Natural reference mode frequencies based on [bib1]
m=1 |
FF (Hz) |
SF (Hz) |
SF (Hz) |
SS (Hz) |
CS (Hz) |
CC (Hz) |
n=1 |
598,846 |
415,756 |
415,756 |
272,118 |
391,746 |
559,562 |
n=2 |
654,216 |
657,308 |
657,308 |
663,543 |
671,113 |
687,249 |
n=3 |
1850,287 |
1851,807 |
1851,807 |
1855,440 |
1856,454 |
1858,296 |
n=4 |
3547,660 |
3549,113 |
3549,113 |
3552,948 |
3553,286 |
3553,911 |
n=5 |
5737,228 |
5738,698 |
5738,698 |
5742,737 |
5742,872 |
5743,210 |
n=6 |
8416,323 |
8417,793 |
8417,793 |
8421,966 |
8422,000 |
8422,237 |
To complete the analytical solutions of this problem, we cite [bib2] which compares a dozen shell theories. It also highlights the shapes of the eigenmodes based on the values \(m\) and \(n\) (Fig. 3). For the case of the SS limit condition, we find a consistency of the results (\(\mathrm{\lambda }\)) during \(n\) =1,2,3 and \(m\) =1 (marked as a black spot on curve 2 in Fig. 4, \(l/\mathit{mR}\) =20 corresponding to our case).
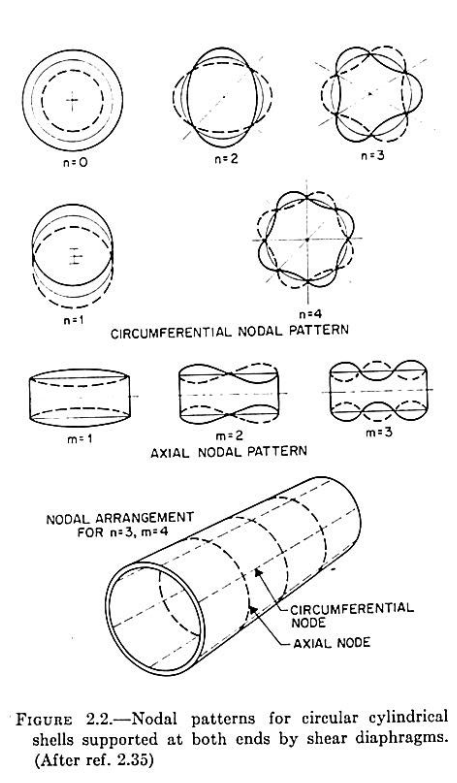
Fig. 3. Scheme of eigenmodes as a function of \(m\) and \(n\) in [bib2]
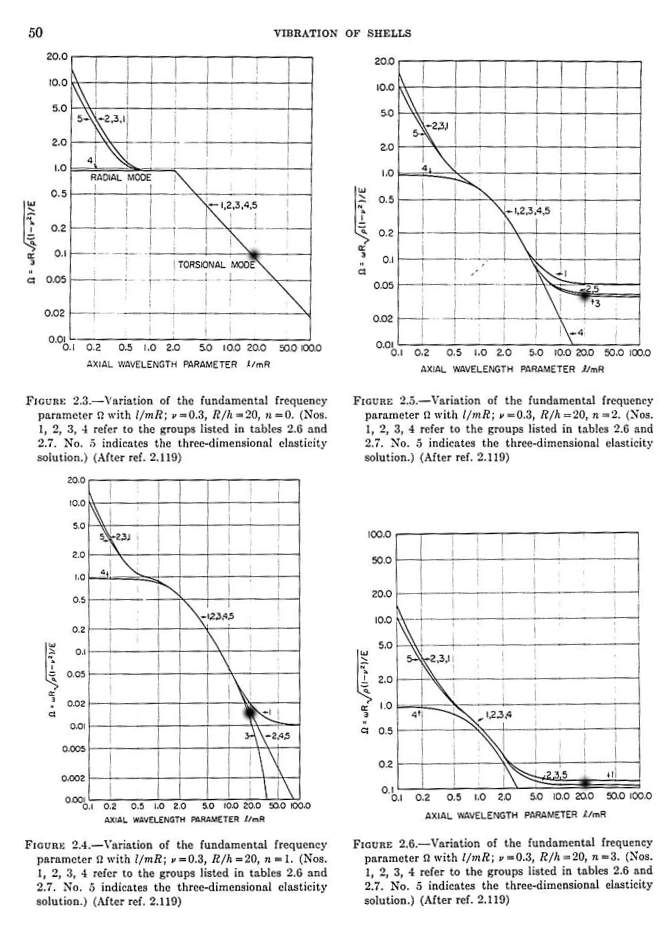
Fig. 4. Comparison of the evolution \(\mathrm{\lambda }\) of as a function of \(l/\mathit{mR}\) between different shell theories for the SS case in [bib2]: curve 2 for the Goldenveizer-Novozhilov theory
2.2. Bibliographical references#
XIE, G. JIN, Z. LIU: Free vibration analysis of cylindrical shells using the haar wavelet method, International Journal of Mechanical Sciences 77 (2013) 47-56.
LEISSA: Vibration of shells. Ohio State University, 1973.