4. B modeling#
4.1. Characteristics of modeling#
This modeling is identical to the previous one except that the natural modes of the complete system are calculated using the modal calculation method by substructuring with “MacNeal” interfaces (free interfaces). The bases of each substructure are composed of a dynamic mode and an attachment mode.
The transient response of the system is calculated on the modal basis calculated by substructuring.
More precisely, the substructures studied have their interfaces free of charge:
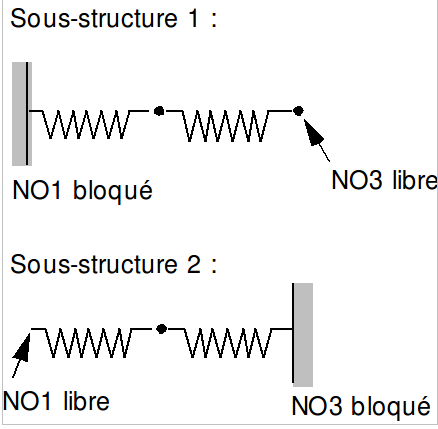
The time steps used are: \({10}^{-2}s\) in EULER, \({10}^{-2}s\) in NEWMARK, in, \({10}^{-2}s\) in DEVOGE, \({10}^{-2}s\) in ADAPT_ORDRE2 (for the latter, it is the initial time step of the algorithm and the maximum time step is set to the formula \(\mathrm{0,1}s\) in order to optimize the calculation time).
4.2. Characteristics of the substructure mesh#
Number of knots: 3
Number of meshes and types: 2 SEG2
4.3. Tested sizes and results#
Identification |
Reference |
Method: EULER |
|
Node \({x}_{2}\), displacement (\(m\)) |
4.1700 10—1 |
Knot \({x}_{2}\), speed (\({\mathrm{m.s}}^{-1}\)) |
—4.3011 10—1 |
Node \({x}_{2}\), acceleration (\({\mathrm{m.s}}^{-2}\)) |
3.3749 10—1 |
Method: NEWMARK |
|
Node \({x}_{2}\), displacement (\(m\)) |
4.1700 10—1 |
Knot \({x}_{2}\), speed (\({\mathrm{m.s}}^{-1}\)) |
—4.3011 10—1 |
Node \({x}_{2}\), acceleration (\({\mathrm{m.s}}^{-2}\)) |
3.3749 10—1 |
Method: DEVOGE |
|
Node \({x}_{2}\), displacement (\(m\)) |
4.1700 10—1 |
Knot \({x}_{2}\), speed (\({\mathrm{m.s}}^{-1}\)) |
—4.3011 10—1 |
Node \({x}_{2}\), acceleration (\({\mathrm{m.s}}^{-2}\)) |
3.3749 10—1 |
Method: ADAPT_ORDRE2 |
|
Node \({x}_{2}\), displacement (\(m\)) |
4.1700 10—1 |
Knot \({x}_{2}\), speed (\({\mathrm{m.s}}^{-1}\)) |
—4.3011 10—1 |
Node \({x}_{2}\), acceleration (\({\mathrm{m.s}}^{-2}\)) |
3.3749 10—1 |