3. Modeling A#
3.1. Characteristics of modeling#
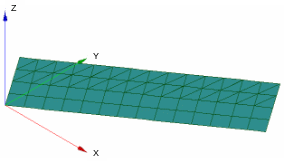
35°
48.24°
NO. 1
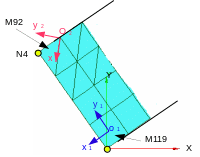
X
Y
O
3.2. Characteristics of the mesh#
Number of knots: 75
Number of meshes and type: 28 QUAD4 56 TRIA3
3.3. Tested sizes and results#
Modeling DKT
The quantities are expressed in the coordinate system \(xoy\)
Maille |
Bow |
Grandeur |
Reference type |
Reference |
Tolerance |
|
\(\mathit{M119}\) |
\(\mathit{N1}\) |
EFGE_ELNO |
\(\mathit{NXX}\) |
“ANALYTIQUE” |
\(1.25\mathrm{\times }{10}^{6}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{NXY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{MXX}\) |
“ANALYTIQUE” |
\(\mathrm{-}7.8125\mathrm{\times }{10}^{5}N\) |
\(0.01\text{\%}\) |
|||
\(\mathit{MYY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}4}\) |
|||
\(\mathit{MXY}\) |
“ANALYTIQUE” |
\(0.0\) |
\(50\) |
|||
\(\mathit{M92}\) |
\(\mathit{N4}\) |
EFGE_ELNO |
\(\mathit{NXX}\) |
“ANALYTIQUE” |
\(1.25\mathrm{\times }{10}^{6}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{NXY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{MXX}\) |
“ANALYTIQUE” |
\(\mathrm{-}7.8125\mathrm{\times }{10}^{5}N\) |
\(5.\text{\%}\) |
|||
\(\mathit{MYY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{MXY}\) |
“ANALYTIQUE” |
\(0.0\) |
\(300\) |
|||
The quantities are expressed in the coordinate system \({x}_{1}{o}_{1}{y}_{1}\)
Maille |
Bow |
Grandeur |
Reference type |
Reference |
Tolerance |
|
\(\mathit{M119}\) |
\(\mathit{N1}\) |
EFGE_ELNO |
\(\mathit{NXX}\) |
“ANALYTIQUE” |
\(1.25\mathrm{\times }{10}^{6}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{NXY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{MXX}\) |
“ANALYTIQUE” |
\(\mathrm{-}7.8125\mathrm{\times }{10}^{5}N\) |
\(0.01\text{\%}\) |
|||
\(\mathit{MYY}\) |
“ANALYTIQUE” |
\(0.0\) |
\({10}^{\mathrm{-}6}\) |
|||
\(\mathit{MXY}\) |
“ANALYTIQUE” |
\(0.0\) |
\(50\) |
|||
The quantities are expressed in the coordinate system \({x}_{2}{o}_{2}{y}_{2}\)
Maille |
Bow |
Grandeur |
Reference type |
Reference |
Tolerance |
|
\(\mathit{M92}\) |
\(\mathit{N4}\) |
EFGE_ELNO |
\(\mathit{NXX}\) |
“ANALYTIQUE” |
\(5.4471\mathrm{\times }{10}^{5}N\mathrm{/}m\) |
\({10}^{\mathrm{-}4}\) |
\(\mathit{NYY}\) |
“ANALYTIQUE” |
\(6.9553\mathrm{\times }{10}^{5}N\mathrm{/}m\) |
\({10}^{\mathrm{-}4}\) |
|||
\(\mathit{NXY}\) |
“ANALYTIQUE” |
\(6.2101\mathrm{\times }{10}^{5}N\mathrm{/}m\) |
\({10}^{\mathrm{-}4}\) |
|||
\(\mathit{MXX}\) |
“ANALYTIQUE” |
\(\mathrm{-}3.4654\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}2}\) |
|||
\(\mathit{MYY}\) |
“ANALYTIQUE” |
\(\mathrm{-}4.3471\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}2}\) |
|||
\(\mathit{MXY}\) |
“ANALYTIQUE” |
\(\mathrm{-}3.8813\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}2}\) |
|||
Q4GG modeling
The quantities are expressed in the coordinate system \(xoy\)
Maille |
Point |
Grandeur |
Reference type |
Reference |
Tolerance |
|
\(\mathit{M119}\) |
\(3\) |
SIEF_ELGA |
\(\mathit{NXX}\) |
“NON_REGRESSION” |
\(1.25\mathrm{\times }{10}^{6}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{NXY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXX}\) |
“NON_REGRESSION” |
\(\mathrm{-}7.53348\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MYY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{M92}\) |
\(1\) |
SIEF_ELGA |
\(\mathit{NXX}\) |
“NON_REGRESSION” |
\(1.25\mathrm{\times }{10}^{6}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{NXY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXX}\) |
“NON_REGRESSION” |
\(\mathrm{-}7.53349\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MYY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
The quantities are expressed in the coordinate system \({x}_{1}{o}_{1}{y}_{1}\)
Maille |
Point |
Grandeur |
Reference type |
Reference |
Tolerance |
|
\(\mathit{M119}\) |
\(3\) |
SIEF_ELGA |
\(\mathit{NXX}\) |
“NON_REGRESSION” |
\(1.25\mathrm{\times }{10}^{6}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{NXY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXX}\) |
“NON_REGRESSION” |
\(\mathrm{-}7.5346\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MYY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXY}\) |
“NON_REGRESSION” |
\(0.0\) |
\({10}^{\mathrm{-}10}\) |
|||
The quantities are expressed in the coordinate system \({x}_{2}{o}_{2}{y}_{2}\)
Maille |
Point |
Grandeur |
Reference type |
Reference |
Tolerance |
|
\(\mathit{M92}\) |
\(1\) |
SIEF_ELGA |
\(\mathit{NXX}\) |
“NON_REGRESSION” |
\(5.54471\mathrm{\times }{10}^{5}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
\(\mathit{NYY}\) |
“NON_REGRESSION” |
\(6.95529\mathrm{\times }{10}^{5}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{NXY}\) |
“NON_REGRESSION” |
\(6.21007\mathrm{\times }{10}^{5}N\mathrm{/}m\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXX}\) |
“NON_REGRESSION” |
\(\mathrm{-}3.34169\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MYY}\) |
“NON_REGRESSION” |
\(\mathrm{-}4.19180\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}10}\) |
|||
\(\mathit{MXY}\) |
“NON_REGRESSION” |
\(\mathrm{-}3.74269\mathrm{\times }{10}^{5}N\) |
\({10}^{\mathrm{-}10}\) |
|||