1. Reference problem

1.1. Geometry

We consider a cube of size \(10\mathrm{\times }10\mathrm{\times }10\mathit{mm}\) that has a crack on one of its sides (figure).

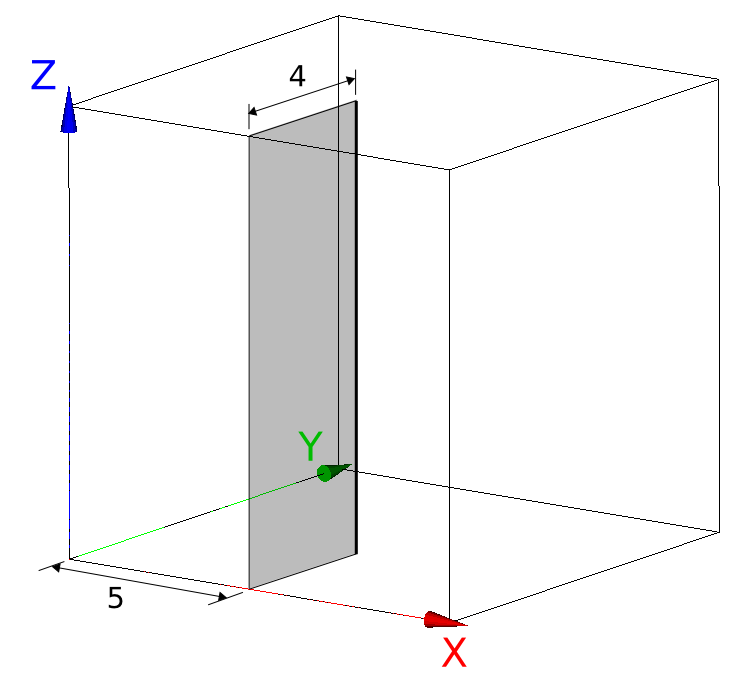
Figure 1.1-a : cracked geometry of the structure

1.2. Material properties

A material with the following elastic properties is used: \(E\mathrm{=}70000\mathit{MPa}\) and \(\nu \mathrm{=}0.34\).

These properties are used by PROPA_FISS to calculate the number of fatigue cycles. However, the finite element model is not solved and there is no need to calculate the number of cycles, which makes the choice of material properties arbitrary.

1.3. Boundary conditions and loads

No boundary conditions are defined because we do not solve the finite element model: we will calculate a propagation in \(I\) mode of the existing crack with imposed and constant displacement along the bottom. The crack remains flat during propagation.

An advance equal to \(\Delta a=1\mathrm{mm}\) is being imposed. The bottom of the crack spreads while always staying straight.

1.4. Initial conditions

The initial crack is a half-plane. Its length is equal to \({a}_{0}\mathrm{=}4\mathit{mm}\). The bottom of the crack is straight.