1. Reference problem#
1.1. Geometry#
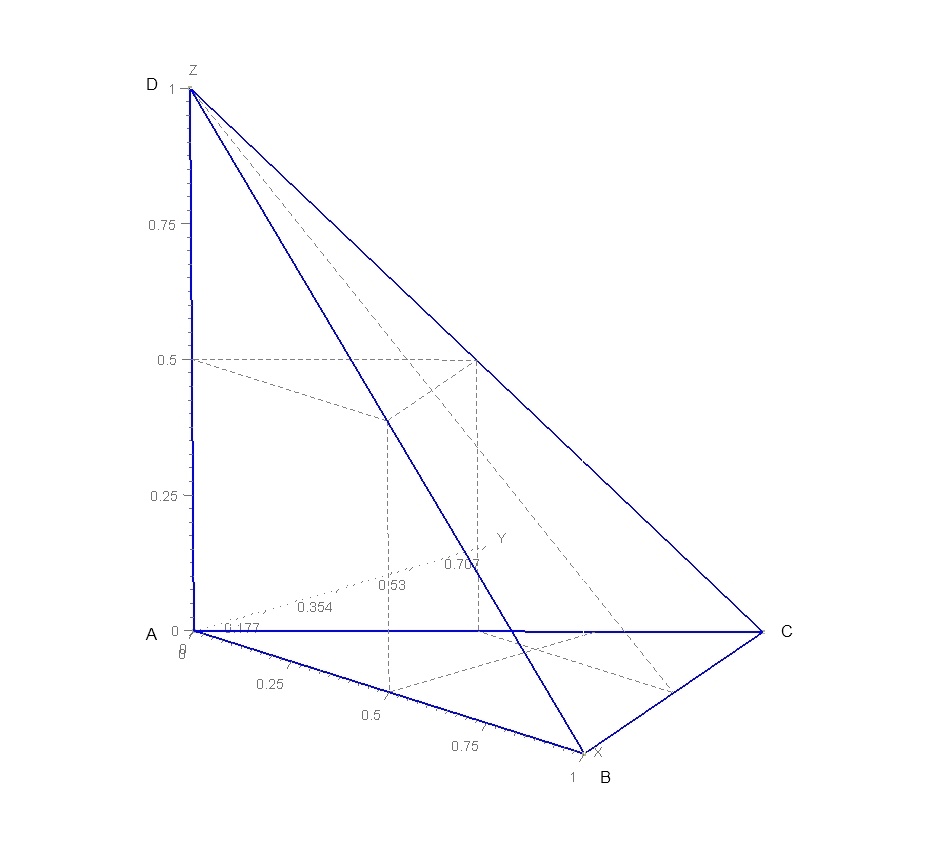
Figure 1.1-1 : Representation of geometry
Point \(A\): |
\((\mathrm{0,0}\mathrm{,0})\) |
Point \(B\): |
\((\mathrm{1,0}\mathrm{,0})\) |
Point \(C\): |
\((\frac{\sqrt{(2)}}{2},\frac{\sqrt{(2)}}{2}\mathrm{,0})\) |
Point \(D\): |
\((\mathrm{0,0}\mathrm{,1})\) |
Table 1.1-1 : Point coordinates
1.2. Material properties#
The material is steel:
\(E\mathrm{=}2.04{10}^{11}\), \(\nu \mathrm{=}0.3\), \(\alpha =1.092{10}^{-5}\).
1.3. Boundary conditions and loads#
1.3.1. Loading on a vertical edge (support for one of the axes of the coordinate system)#
The validation of the ARETE_IMPO keyword must require the equivalence of the following conditions:
1.3.1.1 conditions:
Face \(\mathrm{DBC}\) imposed: \(\mathrm{DNOR}=10\)
Deadlock at points \(D,B,C\): \(\mathrm{DX}=\mathrm{0,}\mathrm{DY}=\mathrm{0,}\mathrm{DZ}=0\)
Displacement imposed on the nodes of the \(\mathrm{DA}\) edge: \(\mathrm{DZ}=0\)
1.3.1.2 conditions:
Face \(\mathrm{DBC}\) imposed: \(\mathrm{DNOR}=10\)
Deadlock at points \(D,B,C\): \(\mathrm{DX}=\mathrm{0,}\mathrm{DY}=\mathrm{0,}\mathrm{DZ}=0\)
Imposed \(\mathrm{DA}\) edge: \(\mathrm{DTAN}=0\) except at point \(D\).
We will validate the equivalence between these conditions by testing the movements at node \(A\).
1.3.2. Loading on oblique edges#
The validation of the ARETE_IMPO keyword must require the equivalence of the following conditions:
1.3.2.1 conditions:
Blocking at the nodes on the face \(\mathrm{ABC}\): \(\mathrm{DX}=\mathrm{0,}\mathrm{DY}=\mathrm{0,}\mathrm{DZ}=0\)
Displacement imposed at the nodes of edge \(\mathrm{DA}\): \(\mathrm{DZ}=-1\) (except at points \(D\) and \(A\))
Oblique connection to the nodes of edge \(\mathrm{DB}\) (except at points \(D\) and \(B\)): \(\mathrm{DX}=1\), \(\mathrm{ANGL}\text{\_}\mathrm{NAUT}=(\mathrm{0,45}\mathrm{,0})\)
Oblique connection to the nodes of edge \(\mathrm{DC}\) (except at points \(D\) and \(C\)): \(\mathrm{DX}=1\), \(\mathrm{ANGL}\text{\_}\mathrm{NAUT}=(\mathrm{45,45}\mathrm{,0})\)
1.3.2.2 conditions:
Blocking at the nodes on the face \(\mathrm{ABC}\): \(\mathrm{DX}=\mathrm{0,}\mathrm{DY}=\mathrm{0,}\mathrm{DZ}=0\)
Imposed \(\mathrm{DA}\) edge: \(\mathrm{DTAN}=1\) except at points \(D\) and \(A\).
Imposed \(\mathrm{DB}\) edge: \(\mathrm{DTAN}=1\) except at points \(D\) and \(B\).
Imposed \(\mathrm{DC}\) edge: \(\mathrm{DTAN}=1\) except at points \(D\) and \(C\).
We will validate the equivalence between these conditions by testing the movements at node \(D\).