4. B modeling#
4.1. Mechanical results#
The elastic prediction method (PRED_ELAS) is used. The force-displacement curve obtained is in the. The test piece at time \(C\) is completely broken, with the residual force being close to zero. It is at this moment that the crack opening will be calculated. The pattern of the movements and of the damage are given in Figures and.

Figure 4.1-1: Force-displacement curve, bi-notched specimen (law ENDO_SCALAIRE).
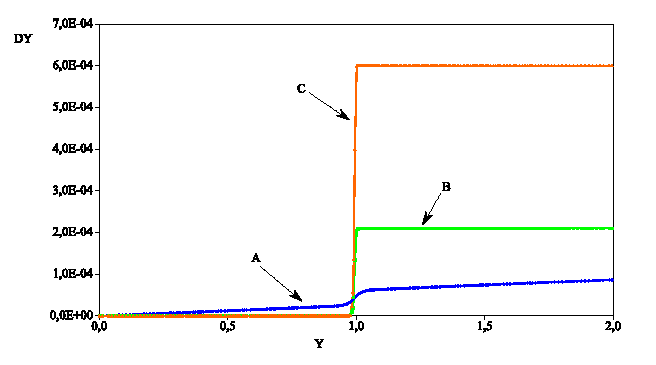
Figure 4.1-2: Displacements along the longitudinal axis of the specimen (law ENDO_SCALAIRE).
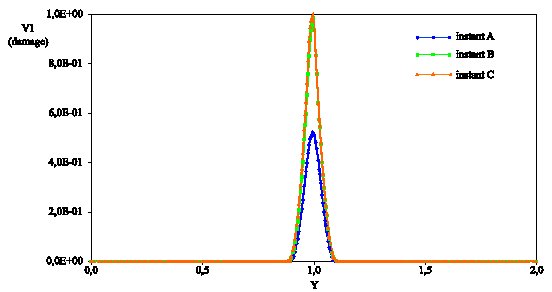
Figure 4.1-3: Damage on the longitudinal axis of the specimen (law ENDO_SCALAIRE).
4.2. Tested sizes and results#
The crack path found at instant \(C\) is shown in the for component VARI of field DEPL. The path found with field VARI_NOEU is similar.
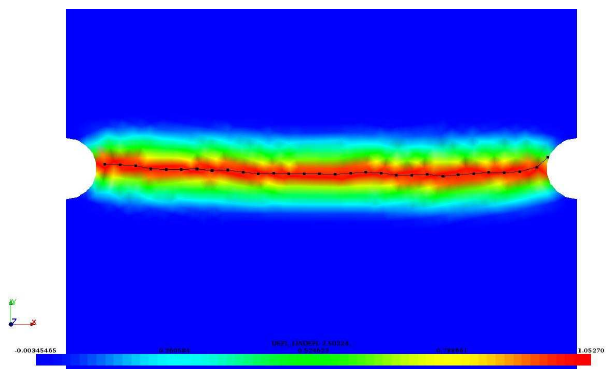
Figure 4.2-1: crack path in the bi-notched specimen (law ENDO_SCALAIRE).
At the end of the calculation, either the crack path or the crack opening are tested.
As far as the cracking path is concerned, this path must in principle be located on the axis of symmetry of the test piece, on the axis \(x\). It is then tested that the maximum distance from this axis of the points found by the command is less than a certain precision. An analytical test case is planned, with (absolute) precision equal to \(1.5\mathrm{\times }\mathit{taille}\mathit{élément}\mathrm{=}0.03m\).
As far as the crack opening is concerned, this must be equal to rupture at the imposed displacement. We therefore propose an analytical test case, with relative accuracy of 10%, and a non-regression test case with 5% accuracy.
In summary, if we use field VARI_NOEU, component \(\mathit{V1}\) to search for the crack path:
Quantity tested |
Test type |
Precision requested |
Test case precision |
\(\mathit{DY}\) |
Analytics |
\(0.03m\) |
|
Openness |
Analytics |
:math:`10`% |
:math:`4.69`% |
Openness |
Non-regression |
:math:`5`% |
:math:`4.69`% |
If we use field DEPL, component VARI to search for the crack path:
Quantity tested |
Test type |
Precision requested |
Test case accuracy |
\(\mathit{DY}\) |
Analytics |
\(0.03m\) |
|
Openness |
Analytics |
:math:`10`% |
:math:`4.97`% |
Openness |
Non-regression |
:math:`5`% |
:math:`4.97`% |
4.3. notes#
The crack path found is satisfactory, however the precision found is at the limit of the accuracy allowed for the analytical test case. This is due to the fact that law ENDO_SCALAIRE very much locates damage when approaching breakage (damage=1). In fact, according to analytical solutions, the damage is equal to 1 for the crack. This requires very fine meshes in the location band. In the, a more accurate crack path could have been obtained as a result of a mechanical calculation using a finer mesh.
For crack opening, the sources of error are related to:
cracking path not perfectly straight,
residual force on the test piece that is close but not equal to zero.